Замкнутый электрический привод с частотным управлением асинхронного двигателя

Замкнутая схема импульсного регулирования скорости асинхронного двигателя с помощью резистора в цепи ротора

Замкнутый электрический привод с частотным управлением асинхронного двигателя

Вопросы

Двигателями переменного тока

Замкнутые схемы управления электроприводов с

ЛЕКЦИЯ 12

1) Замкнутая схема управления асинхронного электропривода, выполненного по системе «тиристорный регулятор напряжения—асинхронный двигатель» (ТРН—АД)

По исторически сложившейся тенденции регулируемый ЭП строился главным образом с использованием ДПТ. В последние годы в связи с появлением разнообразных средств управления регулируемый ЭП переменного тока начал быстро вытеснять АЭП с ДПТ.

1 Замкнутая схема управления асинхронного электропривода, выполненного по системе «тиристорный регулятор напряжения—асинхронный двигатель» (ТРН—АД)

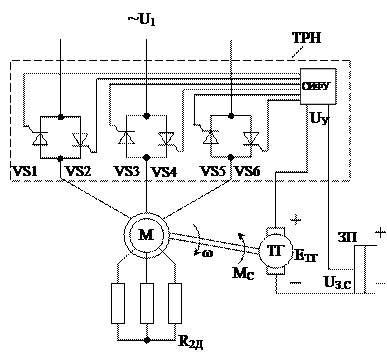
Рассмотрим схему регулирования скорости АД с фазным ротором с использованием обратной связи по его скорости (рис.1,а). Между сетью и статором АД включены три пары встречно-параллельно соединенных тиристоров VS1 — VS6, образующих силовую часть ТРН. Управляющие электроды тиристоров подсоединены к выходам системы импульсно-фазового управления (СИФУ), которая распределяет управляющие импульсы на все тиристоры и осуществляет их сдвиг в зависимости от сигнала управления U_y. К валу АД подсоединен тахогенератор ТГ. Его ЭДС Е_тг сравнивается с задающим напряжением U_з.с, снимаемым с задающего потенциометра скорости ЗП, причем эти напряжения включены навстречу друг другу. Разность напряжений U_3.C и Е_гг, равная напряжению управления

поступает на вход СИФУ.

При увеличении этого сигнала угол управления тиристорами уменьшается, а подаваемое на АД напряжение увеличивается и наоборот. В цепь ротора АД постоянно включен добавочный резистор R_2Д, наличие которого позволяет расширить диапазон регулирования скорости и облегчить тепловой режим АД при его работе на пониженных скоростях.

Рассмотрим работу ЭП при изменении момента нагрузки М_с на валу АД и постоянном задании скорости сигналом U_3.С2. Допустим также, что в исходном положении АД работал в точке 1 при моменте нагрузки M_С1 (рис. 1,б), а затем произошло его увеличение до значения М_С2.

При увеличении нагрузки на валу АД его скорость начнет снижаться, соответственно начнет уменьшаться и ЭДС тахогенератора Е_ТГ. Уменьшение Е_тг вызывает согласно (1) увеличение напряжения управления, что приведет к уменьшению угла отпирания тиристоров и увеличению тем самым подаваемого на АД напряжения.

а)

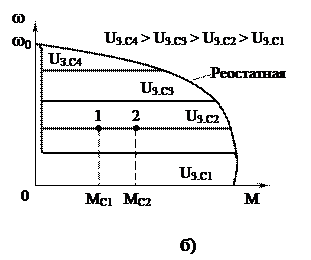Рисунок 1 — Схема (а) замкнутой системы ТРН—АД и механические характеристики (б)

Момент АД будет увеличиваться и в точке 2 сравняется с М_С2. Таким образом, увеличение момента нагрузки привело к небольшому снижению скорости АД, т. е., другими словами, его характеристики стали жесткими.

При уменьшении момента нагрузки М_с будет автоматически происходить снижение напряжения на АД и тем самым поддержание его скорости вращения на заданном уровне.

Изменяя с помощью потенциометра значение задающего напряжения U_3.С, можно получить ряд механических характеристик электропривода с относительно высокой жесткостью и необходимой перегрузочной способностью АД.

Примером замкнутого ЭП переменного тока может служить серия ЭКТ и ее модернизация ЭКТ2. Эти ЭП обеспечивают регулирование скорости, тока и момента трехфазных АД с короткозамкнутым ротором за счет изменения частоты и величины подводимого к нему напряжения. Упрощенная функциональная схема этого ЭП в однолинейном исполнении приведена на рисунке 2, а.

В качестве силового преобразователя в ЭП используется тиристорный преобразователь частоты со звеном постоянного тока, состоящий из управляемого выпрямителя (УВ) и инвертора напряжения (ИН) со своими схемами управления СУВ и СУИ. Между УВ и ИН включен силовой фильтр Ф, обеспечивающий фильтрацию выходного напряжения и циркуляцию реактивной мощности в силовой части схемы.

Схема управления ЭП построена по принципу подчиненного регулирования координат и имеет два контура — внутренний (тока) и внешний (напряжения). Регулирование этих координат осуществляется пропорционально-интегральными регуляторами тока РТ и напряжения РН, по сигналам датчиков тока ДТ и напряжения ДН. При частотах ниже номинальной схема управления поддерживает отношение напряжения к частоте постоянным, а при частотах выше номинальной напряжение остается неизменным, что обеспечивается усилителем — ограничителем УО.

Преобразователь частоты обеспечивает рабочие диапазоны изменения частоты (5. 80) Гц при номинальной частоте 50 Гц и (15. 240) Гц при номинальной частоте 200 Гц. Диапазон регулирования напряжения составляет (0. 380) В. Серия ЭКТ2 выпускается на мощности от 16,5 до 263,5 кВт. КПД этих ЭП лежит в пределах (85. 96)%.

Примерный вид механических характеристик ЭП при различных сигналах задания скорости приведены на рисунке 2, б.

ЭП этой серии могут обеспечивать торможение с рекуперацией энергии в сеть. В этом случае силовая часть ЭП дополняется ведомым сетью инвертором, а в обозначении ЭП появляется буква Р (ЭКТР и ЭКТ2Р).

а)

б)

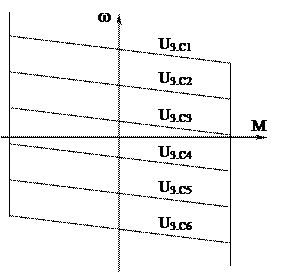Рисунок 2 — Схема (а) замкнутого ЭП с частотным управлением АД и механические характеристики (б)

ЗАМКНУТЫЕ СИСТЕМЫ УПРАВЛЕНИЯ АСИНХРОННЫМИ ЭЛЕКТРОПРИВОДАМИ С ПОЛУПРОВОДНИКОВЫМИ ПРЕОБРАЗОВАТЕЛЯМИ

Как показано в ряде работ [6, 76—78, 83, 84], при применении замкнутых САУ удается значительно расширить функциональные возможности асинхронных электроприводов с полупроводниковыми преобразователями и обеспечить качественно новые свойства си­стем параметрического управления асинхронными двигателями. Используя в зависимости от технических требований различные виды обратных связей — по скорости; положению, току ротора (для двигателей с контактными кольцами) и статора, можно реализо­вать управляемые пускотормозные режимы, плавное регулирова­ние скорости в широких пределах, позиционирование производст­венных механизмов и т. д.

Для обеспечения требуемого качества замкнутых САУ в пере­ходных и установившихся режимах необходимо располагать обо­снованными методами анализа и синтеза таких систем, основанны­ми на изучении динамических свойств элементов, входящих в САУ, и, в первую очередь, методами исследования асинхронного дви­гателя как объекта регулирования.

Так как при управлении от полупроводниковых преобразовате­лей осуществляется импульсное воздействие на асинхронный дви­гатель, то момент асинхронного двигателя даже при установив­шейся скорости имеет пульсирующий характер и содержит глад­кую и переменную составляющие. Частота пульсаций последней (fn) зависит от схемы преобразователя. В рациональных схемах преобразователей, включаемых в статорные цепи для регулирова­ния переменного напряжения (см. рис. 1.1,а; 1.2,6), /п^300 Гц при fo—50 Гц; в преобразователях, предназначенных для реали­зации режима динамического торможения (см. рис. 1.8,в, г), /п^ЮО Гц при fo=50 Гц и в преобразователях для импульсного управления в роторных цепях (см. рис. 1.5,a) fn^ЗОО-МЮО Гц. Очевидно, указанные значения fn значительно выше реально до­стижимой полосы пропускания (fnp) непрерывной части системы автоматического управления, так что всегда выполняется условие

позволяющее свести импульсное звено к непрерывному [79], т. е. пульсирующая составляющая момента не может оказать сколько — нибудь заметного влияния на динамические показатели САУ. В свя­

зи с этим полупроводниковые преобразователи можно рассматри­вать как непрерывное звено, на выходе которого регулируется по­лезная составляющая управляющего воздействия, определяющая постоянную (среднюю) составляющую момента асинхронного дви­гателя. Укажем, что возможность рассмотрения систем с полупро­водниковыми преобразователями путем выделения непрерывной полезной составляющей обоснована в [80].

В системах параметрического управления необходимо исследо­вать частотные характеристики асинхронного двигателя при сле­дующих способах воздействия:

1) регулировании первой гармоники переменного напряжения (РПН), прикладываемого к статорным цепям двигателя. В этом случае изменяются действующее значение (Vі*) и амплитуда (Um) основной гармоники;

2) регулировании выпрямленного (постоянного) напряжения (РВН), когда изменяется значение Un в режиме динамического торможения;

3) регулировании добавочного сопротивления (РДС) в роторе асинхронного двигателя с контактными кольцами.

Вначале исследуем динамические характеристики асинхронного двигателя при его упрощенном описании без учета электромагнит­ных переходных процессов; такой подход используется в ряде ра­бот [81, 83, 85].

Выражения (3.36), (3.61) позволяют определить установивший­ся момент асинхронных короткозамкнутых двигателей. Для двига­телей с контактными кольцами способы управления, связанные с регулированием переменного или постоянного напряжения, могут быть реализованы при введении добавочных невыключаемых со­противлений в роторную цепь (і?2д) • Кроме того, может быть осу­ществлено регулирование R? д. В этих случаях изменяется суммар­ное активное сопротивление роторной цепи ^22==^2+^2д — Для удобства дальнейшего рассмотрения целесообразно ввести без­размерный коэффициент r = /?22/i?2= (#2 + #2д)/#2 [81]. ОчЄВИДНО, для короткозамкнутых двигателей г— 1, при использовании спо­собов управления РПН и РВН для двигателей с контактными кольцами г>1, r=const, при реализации способа РДС г^1, r=var. При включении добавочных сопротивлений изменяются коэффициенты затухания роторного контура arz=R’22,/Xr и a’rx = R,2z/cXr по сравнению с аналогичными величинами для ко­роткозамкнутого ротора (ar=R’ъ/Хг и a’r=Rf2lоХг), однако при введении коэффициента г они связаны простой зависимостью: а’гл — агг, arz=arr. С учетом этого запишем выражения для уста­новившегося момента асинхронного двигателя при различных спо­собах параметрического управления:

т _ _____________ Um2_ (1 — a)a/rs________________ Uт2 (Г — о)ar’rs

aXs [(а/а/ro — s)2 -f (а/r+а/ ,s)a] as Xs (a2 + b2)

где a=a’sa’rrc—s; fc = a/rr+!a’ss;

рдс, когда к статору приложено номинальное напряжение се­ти (Um= 1)

Выражения (4.2) — (4.4), являющиеся уравнениями статических механических характеристик асинхронного двигателя, можно при­вести к форме записи в виде формул Клосса. Так, при регулиро­вании первой гармоники переменного напряжения выражение для момента может быть записано в следующем виде:

щ _ 2mK(l j — е)__________________ 2тк>б(1 -)- e)Um2 ^ ^

s/sk + sK/s — f — 2е s/sK sK/s — f — 2є

где mK — критический момент двигателя на регулировочной ха­рактеристике; тК)б — критический момент двигателя на естествен­ной (базовой) характеристике, когда Um= 1; є — конструктивный коэффициент двигателя.

Переходя от (4.2) к (4.5), получаем:

s„ = *r’rVi(a; o’ +1)/(«/ +1) = arr 1/(0./ + l)/(a/ + 0“); (4.7) . = a/ (1 _ a) / Y(a/ + 1) (a/ + 1). (4.8)

Значение тк, б определяется из (4.6) при подстановке в него Um=. При регулировании добавочного сопротивления в роторе в (4.5) также нужно брать Um= 1.

Для режима динамического торможения формула Клосса за­писывается в следующем виде:

т=2тк, д>т/ (юк/со+ш/сок) =

= 2тк, б,д, тС/п2/ (юк/со+со/сок), (4.9)

где тк, д>Т, сок — критический момент и скорость в режиме динами­ческого торможения; тк, б.д. т — критический момент динамического торможения на базовой характеристике, когда Un= 1.

Приводя (4.4) к виду (4.9), получаем:

тк, д>т = — ипЦ-о)/ (6Xsas2); (4.10)

Значение тК)б, д,т определяется из (4.10) при подстановке в не­го Un= 1.

Для исследования динамических свойств асинхронного двига­теля используем также уравнение динамики электропривода

Как видно из (4.2) — (4.4), даже при упрощенном описании асинхронный двигатель является нелинейным объектом, и для анализа частотных характеристик целесообразно воспользоваться методом математической линеаризации нелинейных объектов пу­тем разложения описывающих их уравнений в ряд Тейлора [79], что позволяет, используя теорию линейных САУ, изучить свойства объекта «в малом» при незначительном отклонении переменных от координат центра разложения, соответствующих выбранному уста­новившемуся режиму.

Момент асинхронного двигателя зависит от управляющего воз­действия X и скорости (скольжения) двигателя, т. е. m=fi(X, ю). Очевидно, для РПН X=Um, для РДС Х=г, для РВН X=Un.

Точка установившегося режима характеризуется координатами Ху, coy(sy), ту. Придадим приращение АХ управляющему воздей­ствию в окрестности этой точки. Вследствие этого возникает при­ращение момента Ат и скорости Доз, а также скольжения As. Оп­ределим приращение момента асинхронного двигателя, воспользо­вавшись разложением в ряд Тейлора:

где k=дт/дХ—коэффициент чувствительности момента двига­теля по управляющему воздействию в центре разложения при k (РВН) k2>0r тм>0 и двигатель описывается устойчивым апериодическим звеном в соответствии с (4.15). Если же s>sK (РПН и РДС) или о)>сок (РВН), то &2 1 P2 + ^

2 Зо^а/2 [(arr)2 4- со2]2 p3 4- (a/ 4- a,/r 4- arr)p2 4-

4- <2(1—o)ar, arr2to24-[(afr)2 4- ft>2>[arr(a/-fa/r)—со2]> l+Ky)4—1 4- [arr(2a/ 4- a/r) 4- co2J p 4- 0/ [(arr)2 4- CO2]

Выражение (4.27) можно записать в виде многочлена

Ц7 /р _________________ ^д(Др3 Ч

п B1P5+B! P4 + B„Ps + B«f! + B. P+l ■

I/3aXs a/ [(arr)2 4- a>2] P2 + 2arrp 4- 2 [(arr)2 4- со2]________________

Значения коэффициентов многочлена для различных способов параметрического управления приведены в табл. 4.3.

Определение полюсов и нулей передаточной функции (4.33) для ряда двигателей показывает, что эта функция может быть представлена совокупностью элементарных звеньев первого и вто­рого порядка, что позволяет записать (4.33) в следующем виде:

ІЧР + >) ІЧ2Р2 ±2ЪЧР + 1)

ЧР + 1 (Ч2Р2 + 2Ї4ЧР + 0 (хб2/;2 + %ьЧР + !)