Обсудим сначала вопрос о роли силы трения в движении машины. Представим себе, что водитель машины, стоящей на гладком-гладком льду (сила трения между колесами и льдом отсутствует), нажимает на педаль газа. Что будет происходить? Ясно, что машина ехать не будет: колеса будут вращаться, но будут пробуксовывать относительно льда — ведь трения-то нет. Причем это будет происходить независимо от мощности двигателя. А это значит, что для того, чтобы мощность двигателя использовать, нужно трение — без него машина не поедет.

Что же происходит, когда сила трения есть. Пусть сначала она очень маленькая, а водитель стоящей машины снова нажимает на педаль газа? Колеса (речь сейчас идет о ведущих колесах автомобиля, допустим это передние колеса) проскальзывают относительно поверхности (трение — маленькое), вращаясь так, как показано на рисунке, но при этом возникает сила трения, действующая со стороны дороги на колеса, направленная вперед по ходу движения машины. Она и толкает машину вперед.

Если сила трения большая, то при плавном нажатии на педаль газа колеса начинают вращаться, и как бы отталкиваются от шероховатостей дороги, используя силу трения, которая направлена вперед. При этом колеса не проскальзывают, а катятся по дороге, так, что нижняя точка колеса не перемещается относительно полотна. Иногда и при большом трении колеса пробуксовывают. Наверняка, вы сталкивались с ситуацией, когда какой-нибудь «сумасшедший водитель» так трогается при включении зеленого сигнала светофора, что колеса «визжат», а на дороге остается черный след из-за скольжения резины по асфальту. Итак, в экстренной ситуации (при резком торможении или трогании с побуксовкой) колеса скользят относительно дороги, в обычных случаях (когда на дороге не остается черного следа от стирающихся покрышек) колесо не скользит, а только катится по дороге.

Итак, если машина едет равномерно, то колеса не скользят по дороге, а катятся по ней так, что нижняя точка колеса покоится (а не проскальзывает) относительно дороги. Как в этом случае направлена сила трения? Сказать, что противоположно скорости машины — неверно, ведь говоря так про силу трения, подразумевают случай скольжения тела относительно поверхности, а сейчас у нас скольжения колес относительно дороги нет. Сила трения в этом случае может быть направлена как угодно, и мы сами определяем ее направление. И вот как это происходит.

Представим себе, что нет никаких препятствующих движению машины факторов. Тогда машина движется по инерции, колеса вращаются по инерции, причем угловая скорость вращения колес связана со скоростью движения машины. Установим эту связь. Пусть колесо движется со скоростью $v$ и вращается так, что нижняя точка колеса не проскальзывает относительно дороги. Перейдем в систему отсчета, связанную с центром колеса. В ней колесо как целое не движется, а только вращается, а земля движется назад со скоростью $v$. Но поскольку колесо не проскальзывает относительно земли, то его нижняя точка имеет такую же скорость как земля. А значит, и все точки поверхности колеса вращаются относительно центра со скоростью $v$ и, следовательно, имеют угловую скорость $\omega = v / R$, где R — радиус колеса. Переходя теперь назад в систему отсчета, связанную с землей, заключаем, что при отсутствии проскальзывания между нижней точкой колеса и дорогой угловая скорость колеса $\omega = v / R$, а все точки поверхности имеют разные скорости относительно земли: например, нижняя точка — нулевую, верхняя $2v$ и т. д.

А пусть водитель при таком движении машины нажимает на педаль газа. Он заставляет колесо вращаться быстрее, чем нужно при данной скорости машины. Колесо стремится проскользнуть назад, возникает сила трения, направленная вперед, которая и разгоняет машину (машина как бы отталкивается от шероховатостей дороги, используя силу трения). Если водитель нажимает на педаль тормоза, колесо стремится вращаться медленнее, чем нужно при данной скорости машины. Возникает сила трения, направленная назад, которая тормозит машину. Если водитель поворачивает колеса машины, возникает сила трения, направленная в сторону поворота, которая машину поворачивает. Таким образом, управление машиной — разгоном, торможением, поворотом — основано на правильном использовании силы трения, причем, конечно, подавляющее большинство водителей об этом даже не догадываются.

Ответим теперь на вопрос: равна ли эта сила своему максимальному значению? Вообще говоря, нет, поскольку нет скольжения колеса относительно дороги, а сила трения равна максимальному значению при скольжении. В покое сила трения может принимать любые значения от нуля до максимального $\mu N$, где $\mu$ — коэффициент трения; $N$ — сила реакции опоры. Поэтому если мы разгоняемся (сила трения направлена вперед), но хотим увеличить темп разгона, мы сильнее нажимаем на педаль газа, и увеличиваем силу трения. Аналогично, если мы тормозим (сила трения направлена назад), но хотим увеличить степень торможения, мы сильнее нажимаем на тормоз и увеличиваем силу трения. Но ясно, что ее можно увеличить и в том и в другом случае, если она не была максимальной! Таким образом, для управления машиной сила трения не должна равняться максимальному значению, и эту разность мы используем для совершения тех или иных маневров. И любой водитель (даже если он ничего не знает про силу трения, а таких, конечно, подавляющее большинство) интуитивно чувствует, есть ли у него резерв силы трения, «далеко» ли машина от пробуксовки, и есть ли возможность ей управлять.

Тем не менее, есть одна ситуация, когда сила трения равна своему максимальному значению. Эта ситуация называется заносом. Пусть водитель резко затормозил на скользкой дороге. Машина начинает скользить по дороге, это состояние движения и называется заносом. В этом случае сила трения направлена противоположно скорости (назад) и равна своему максимальному значению. Это ситуация очень опасна, ведь машина АБСОЛЮТНО неуправляема. Мы не можем повернуть (хоть как-то, хоть чуть-чуть), ведь для поворота нам нужна сила трения, направленная в сторону поворота, а в нашем распоряжении ее нет — сила трения максимальна и направлена назад. Мы не можем увеличить скорость торможения (невозможно увеличить силу трения — она и так максимальна), не можем (даже если бы мы захотели этого в такой ситуации) ускориться. Мы не можем ничего! Ситуация осложняется еще и тем, что в состоянии заноса машину никто не «держит» на дороге. Почему машина в обычных условиях не съезжает в кювет, ведь полотно дороги всегда делается покатым к обочинам, чтобы стекала вода? Ее держит сила трения, а вот если машина скользит (занос) сила трения направлена противоположно скорости и никак иначе. Поэтому любое «боковое» возмущение — покатость дороги, небольшой камень под одним из колес — могут развернуть или сбросить машину на обочину. Никогда не допускайте заноса1.

Теперь сравним мощность, которую могут развивать на дороге передне- и заднеприводной автомобили с одинаковым мотором. Очевидно, что мощность, которую может развивать автомобиль на дороге, зависит не только от его двигателя, но и от того, как автомобиль «использует» силу трения. Действительно, в отсутствие силы трения автомобиль стоял бы на месте (с вращающимися колесами) независимо от мощности двигателя (вращающего эти колеса). Докажем, что заднеприводные автомобили мощнее переднеприводных при одинаковой мощности мотора и оценим отношение мощностей, которые может развивать двигатель, разгоняя машину на дороге (при условии, что мощность самого двигателя может быть очень большой).

Разгоняет автомобиль сила трения, действующая на ведущие колеса, а она не может превышать значения $\mu N$ ($N$ — сила реакции). Поэтому чем больше сила реакции, тем больших значений может достигнуть разгоняющая сила трения (а нажатие на педаль газа в ситуации, когда сила трения достигла максимума, приведет только к проскальзыванию и к заносу, но не к увеличению мощности, которую развивает двигатель). Найдем силы реакции для задних и передних колес машины. Силы, действующие на машину при разгоне, показаны на рисунках (на правом — для заднеприводной, на левом — для переднеприводной). На машину действуют: сила тяжести, силы реакции и сила трения. Поскольку машина движется поступательно, сумма моментов всех сил относительно ее центра тяжести равна нулю. Поэтому, если центр тяжести машины находится точно посередине машины, расстояние между задними и передними колесами $l$, а высота центра тяжести над дорогой $h$, условие равенства нулю суммы моментов относительно центра тяжести дает (при условии, что машина движется, развивая максимальную мощность на максимуме силы трения):

$N_ <1>\frac <2>= N_ <2>\frac <2>+ F_ <тр>h = N_ <2>\frac <2>+ \mu N_ <2>h$, (1)

$N_ <1>\frac <2>= N_ <2>\frac <2>+ F_ <тр>h = N_ <2>\frac <2>+ \mu N_<1>h$, (2)

где $\mu$ — коэффициент трения. Учитывая, что и в том и в другом случае $N_ <1>+ N_ <2>= mg$, из (1) найдем силу реакции для передних колес в случае переднеприводного автомобиля

и из (2) силу реакции задних колес в случае заднего привода

(здесь (пп) и (зп) — передний и задний привод). Отсюда находим отношение сил трения, разгоняющих передне- и заднеприводную машину, и, следовательно, отношение мощностей, которые может развивать на дороге их двигатель

Для значений $l = 3 м, h = 0,5 м$ и $\mu = 0,5$ имеем из (5)

Учебники

Журнал «Квант»

Общие

Мякишев Г.Я., Кондрашева Л., Крюков С. Работа сил трения //Квант. — 1991. — № 5. — С. 37-39.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Содержание

Сила трения, как и любая другая сила, совершает работу и соответственно изменяет кинетическую энергию тела при условии, если точка приложения силы перемещается в выбранной системе отсчета. Однако сила трения существенно отличается от других, так называемых консервативных, сил (тяготения и упругости), так как ее работа зависит от формы траектории. Вот почему работу сил трения ни при каких обстоятельствах нельзя представить в виде изменения потенциальной энергии системы. Кроме того, дополнительные сложности при вычислении работы создает специфика силы трения покоя. Здесь существует ряд стереотипов физического мышления, которые хотя и лишены смысла, но очень устойчивы.

Мы рассмотрим несколько вопросов, связанных с не вполне правильным пониманием роли силы трения в изменении энергии системы тел.

О силе трения скольжения

Нередко говорят, что сила трения скольжения всегда совершает отрицательную работу и это приводит к увеличению внутренней (тепловой) энергии системы.

Такое утверждение нуждается в важном уточнении — оно справедливо только в том случае, если речь идет не о работе одной отдельно взятой силы трения скольжения, а о суммарной работе всех таких сил, действующих в системе. Дело в том, что работа любой силы зависит от выбора системы отсчета и может быть отрицательной в одной системе, но положительной в другой. Суммарная же работа всех сил трения, действующих в системе, не зависит от выбора системы отсчета и всегда отрицательна. Вот конкретный пример.

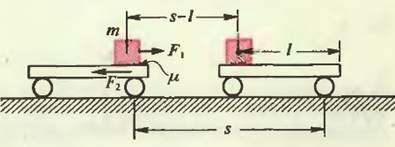
Положим кирпич на движущуюся тележку так, чтобы он начал по ней скользить (рис. 1). В системе отсчета, связанной с землей, сила трения F₁, действующая на кирпич до, прекращения скольжения, совершает положительную работу A₁. Одновременно сила трения F₂, действующая на тележку (и равная по модулю первой силе), совершает отрицательную работу A₂, по модулю большую, чем работа A₁, так как путь тележки s больше пути кирпича s — l (l — путь кирпича относительно тележки). Таким образом, получаем

A_1 = \mu mg(s — l), A_2 = -\mu mgs\) ,

и полная работа сил трения

A_

Поэтому кинетическая энергия системы убывает (переходит в тепло):

\Delta E_k = -\mu mgl\) .

Этот вывод имеет общее значение. Действительно, работа двух сил (не только сил трения), осуществляющих взаимодействие между телами, не зависит от выбора системы отсчета (докажите это самостоятельно). Всегда можно перейти к системе отсчета, относительно которой одно из тел покоится. В ней работа силы трения, действующей на движущееся тело, всегда отрицательна, так как сила трения направлена против относительной скорости. Но она отрицательна и в любой другой системе отсчета. Следовательно, всегда, при любом количестве тел в системе, A_tr О силе трения покоя

При действии между соприкасающимися телами силы трения покоя ни механическая, ни внутренняя (тепловая) энергия этих тел не изменяется. Значит ли это, что работа силы трения покоя равна нулю? Как и в первом случае, такое утверждение правильно только по отношению к полной работе сил трения покоя над всеми взаимодействующими телами. Одна же отдельно взятая сила трения покоя может совершать работу, причем как отрицательную, так и положительную.

Рассмотрим, например, книгу, лежащую на столе в набирающем скорость поезде. Именно сила трения покоя сообщает книге такую же скорость, как у поезда, т. е. увеличивает ее кинетическую энергию, совершая определенную работу при этом. Другое дело, что такая же по модулю, но противоположная по направлению сила действует со стороны книги на стол, а значит, и на поезд в целом. Эта сила совершает точно такую же работу, но только отрицательную. В результате получается, что полная работа двух сил трения покоя равна нулю, и механическая энергия системы тел не меняется.

О движении автомобиля без проскальзывания колес

Самое устойчивое заблуждение связано именно с этим вопросом.

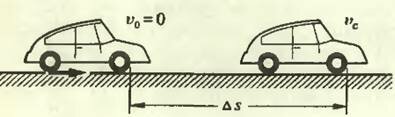
Пусть автомобиль вначале покоится, а затем начинает разгоняться (рис. 2). Единственной внешней силой, сообщающей автомобилю ускорение, является сила трения покоя F_tr действующая на ведущие колеса (мы пренебрегаем силой сопротивления воздуха и силой трения качения). Согласно теореме о движении центра масс, импульс силы трения равен изменению импульса автомобиля:

F_

если скорость центра масс в начале движения равнялась нулю, а в конце υ_c. Приобретая импульс, т. е. увеличивая свою скорость, автомобиль одновременно получает и определенную порцию кинетической энергии. А поскольку импульс сообщается силой трения, естественно считать, что и увеличение кинетической энергии определяется работой этой же силы. Вот это-то утверждение оказывается совершенно неверным. Сила трения ускоряет автомобиль, но работы при этом не совершает. Как же так?

Вообще говоря, ничего парадоксального в этой ситуации нет. В качестве примера достаточно рассмотреть совсем простую модель — гладкий кубик с прикрепленной сбоку пружинкой (рис. 3). Кубик, придвигают к стене, сжимая пружинку, а затем отпускают. «Отталкиваясь» от стены, наша система (кубик с пружинкой) приобретает определенные импульс и кинетическую энергию. Единственной внешней силой, действующей по горизонтали на систему, является, очевидно, сила реакции стены F_p. Именно она и сообщает системе ускорение. Однако никакой работы при этом, конечно, не совершается — ведь точка приложения этой силы неподвижна (в системе координат, связанной с землей), хотя сила действует некоторое конечное время Δt.

Аналогичная ситуация возникает и при разгоне автомобиля без проскальзывания. Точка приложения силы трения, действующей на ведущее колесо автомобиля, т. е. точка соприкосновения колеса с дорогой, в любой момент покоится относительно дороги (в системе отсчета, связанной с дорогой). При движении автомобиля она исчезает в одной точке и сразу же появляется в соседней.

Не противоречит ли сказанное закону сохранения механической энергии? Конечно же, нет. В нашем случае с автомобилем изменение кинетической энергии системы происходит за счет ее внутренней энергии, выделяющейся при сгорании топлива.

Для простоты рассмотрим чисто механическую систему: игрушечный автомобиль с пружинным заводом. Двигатель такого автомобиля использует не внутреннюю энергию топлива, а потенциальную энергию сжатой пружины. Вначале пружина заведена, и ее потенциальная энергия E_p1 отлична от нуля. Если двигатель игрушки — просто растянутая пружина, то \(

E_ = \frac<2>\). Кинетическая энергия равна нулю, и полная начальная энергия автомобиля E₁ = E_p1. В конечном состоянии, когда деформация пружины исчезнет, потенциальная энергия равна нулю, а кинетическая энергия \(

E_ = \frac<2>\). Полная энергия E₂ = E_k2. Согласно закону сохранения энергии (трением мы пренебрегаем),

В случае реального автомобиля

где ΔU — энергия, полученная при сгорании топлива.

Если колеса автомобиля проскальзывают, то A_tr \(

\frac <2>= \frac <2>+ A_

Видно, что кинетическая энергия автомобиля в конечном состоянии оказывается меньше, чем в отсутствие проскальзывания.