Содержание

Тепловая машина карно работа газа за цикл
Физика
Тепловые двигатели. Термодинамические циклы. Цикл Карно

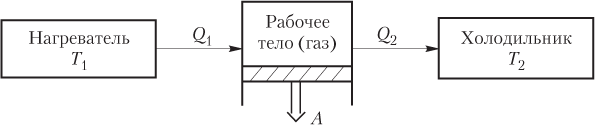
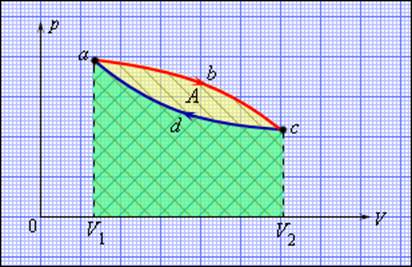
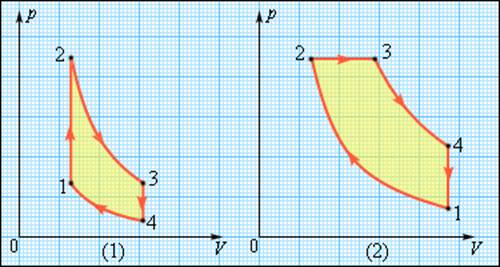
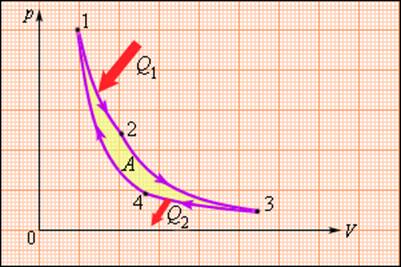
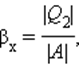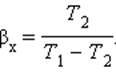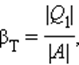Тепловая машина карно работа газа за цикл

Температуру нагревателя тепловой машины Карно понизили, оставив температуру холодильника прежней. Количество теплоты, отданное газом холодильнику за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?

Для каждой величины определите соответствующий характер её изменения:

3) не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

КПД тепловой

машины

Работа газа

КПД тепловой машины Карно вычисляется по формуле: где — соответственно температуры холодильника и нагревателя, — соответственно теплоты, передаваемые холодильнику и отнимаемые от нагревателя. Работа газа в таком процессе: При понижении температуры нагревателя уменьшается КПД тепловой машины, а вместе с ней, при неизменном количестве теплоты, отданном газом холодильнику, уменьшается и работа газа.

Физика

Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.

Цикл работы теплового двигателя состоит из трех этапов:

1) нагреватель передает газу количество теплоты Q 1 ;

2) газ, расширяясь, совершает работу A ;

3) для возвращения газа в исходное состояние холодильнику передается теплота Q 2 .

Из первого закона термодинамики для циклического процесса

где Q — количество теплоты, полученное газом за цикл, Q = Q 1 − Q 2 ; Q 1 — количество теплоты, переданное газу от нагревателя; Q 2 — количество теплоты, отданное газом холодильнику.

Поэтому для идеальной тепловой машины справедливо равенство

Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии

где Q 1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q 2 — теплота, переданная газом холодильнику.

Коэффициент полезного действия тепловой машины вычисляется по одной из формул:

η = A Q 1 ⋅ 100 % , η = Q 1 − Q 2 Q 1 ⋅ 100 % , η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,

где A — работа, совершенная газом; Q 1 — теплота, переданная от нагревателя рабочему телу (газу); Q 2 — теплота, переданная газом холодильнику.

Наиболее часто в тепловых машинах используется цикл Карно , так как он является самым экономичным.

Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.

Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q 1 и происходит изотермическое расширение газа при температуре нагревателя T 1 . Газ совершает положительную работу ( A 12 > 0), его внутренняя энергия не изменяется (∆ U 12 = 0).

Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A 23 приводит к уменьшению внутренней энергии газа: ∆ U 23 = − A 23 , газ охлаждается до температуры холодильника T 2 .

Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q 2 и происходит изотермическое сжатие газа при температуре холодильника T 2 . Газ совершает отрицательную работу ( A 34 U 34 = 0).

Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A 41 приводит к увеличению внутренней энергии газа: ∆ U 41 = − A 41 , газ нагревается до температуры нагревателя T 1 , т.е. возвращается в исходное состояние.

Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:

η = T 1 − T 2 T 1 ⋅ 100 % , η = ( 1 − T 2 T 1 ) ⋅ 100 % ,

где T 1 — температура нагревателя; T 2 — температура холодильника.

Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?

Решение . Коэффициент полезного действия тепловой машины определяется формулой

где A — работа, совершаемая газом за цикл; Q 1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).

Искомой величиной является количество теплоты Q 2 , переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.

Связь между работой A , теплотой Q 1 , переданной от нагревателя газу, и искомой величиной Q 2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины

Уравнения образуют систему

η = A Q 1 ⋅ 100 % , Q 1 = A + Q 2 , >

которую необходимо решить относительно Q 2 .

Для этого исключим из системы Q 1 , выразив из каждого уравнения

Q 1 = A η ⋅ 100 % , Q 1 = A + Q 2 >

и записав равенство правых частей полученных выражений:

A η ⋅ 100 % = A + Q 2 .

Искомая величина определяется равенством

Q 2 = A η ⋅ 100 % − A = A ( 100 % η − 1 ) .

Расчет дает значение:

Q 2 = 400 ⋅ ( 100 % 40 % − 1 ) = 600 Дж.

Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.

Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.

Решение . Для расчета коэффициента полезного действия воспользуемся формулой

η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,

где Q 2 — количество теплоты, которое передается за цикл от газа холодильнику; Q 1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).

Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t :

η = ( 1 − Q 2 / t Q 1 / t ) ⋅ 100 % ,

где Q 2 / t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q 1 / t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).

В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:

Q 1 t = 122 кДж/мин = 122 ⋅ 10 3 60 Дж/с ;

Q 2 t = 30,5 кДж/мин = 30,5 ⋅ 10 3 60 Дж/с .

Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:

η = ( 1 − 30,5 ⋅ 10 3 60 ⋅ 60 122 ⋅ 10 3 ) ⋅ 100 % = 75 % .

Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?

Решение . Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:

до изменения температур нагревателя и холодильника —

η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % ,

где T 1 — первоначальная температура нагревателя; T 2 — первоначальная температура холодильника;

после изменения температур нагревателя и холодильника —

η 2 = ( 1 − T ′ 2 T ′ 1 ) ⋅ 100 % ,

где T ′ 1 — новая температура нагревателя, T ′ 1 = 1,2 T 1 ; T ′ 2 — новая температура холодильника, T ′ 2 = 0,8 T 2 .

Уравнения для коэффициентов полезного действия образуют систему

η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % , η 2 = ( 1 − 0,8 T 2 1,2 T 1 ) ⋅ 100 % , >

которую необходимо решить относительно η 2 .

Из первого уравнения системы с учетом значения η 1 = 25 % найдем отношение температур

T 2 T 1 = 1 − η 1 100 % = 1 − 25 % 100 % = 0,75

и подставим во второе уравнение

η 2 = ( 1 − 0,8 1,2 ⋅ 0,75 ) ⋅ 100 % = 50 % .

Искомое отношение коэффициентов полезного действия равно:

η 2 η 1 = 50 % 25 % = 2,0 .

Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.

Тепловые двигатели. Термодинамические циклы. Цикл Карно

Тепловым двигателем называется устройство, способное превращать полученное количество теплоты в механическую работу. Механическая работа в тепловых двигателях производится в процессе расширения некоторого вещества, которое называется рабочим телом. В качестве рабочего тела обычно используются газообразные вещества (пары бензина, воздух, водяной пар). Рабочее тело получает (или отдает) тепловую энергию в процессе теплообмена с телами, имеющими большой запас внутренней энергии. Эти тела называются тепловыми резервуарами.

Как следует из первого закона термодинамики, полученное газом количество теплоты Q полностью превращается в работу A при изотермическом процессе, при котором внутренняя энергия остается неизменной (ΔU = 0):

Но такой однократный акт преобразования теплоты в работу не представляет интереса для техники. Реально существующие тепловые двигатели (паровые машины, двигатели внутреннего сгорания и т. д.) работают циклически. Процесс теплопередачи и преобразования полученного количества теплоты в работу периодически повторяется. Для этого рабочее тело должно совершать круговой процесс или термодинамический цикл, при котором периодически восстанавливается исходное состояние. Круговые процессы изображаются на диаграмме (p, V) газообразного рабочего тела с помощью замкнутых кривых (рис. 3.11.1). При расширении газ совершает положительную работу A₁, равную площади под кривой abc, при сжатии газ совершает отрицательную работу A₂, равную по модулю площади под кривой cda. Полная работа за цикл A = A₁ + A₂ на диаграмме (p, V) равна площади цикла. Работа A положительна, если цикл обходится по часовой стрелке, и A отрицательна, если цикл обходится в противоположном направлении.

Круговой процесс на диаграмме (p, V). abc – кривая расширения, cda – кривая сжатия. Работа A в круговом процессе равна площади фигуры abcd

Общее свойство всех круговых процессов состоит в том, что их невозможно провести, приводя рабочее тело в тепловой контакт только с одним тепловым резервуаром. Их нужно, по крайней мере, два. Тепловой резервуар с более высокой температурой называют нагревателем, а с более низкой – холодильником. Совершая круговой процесс, рабочее тело получает от нагревателя некоторое количество теплоты Q₁ > 0 и отдает холодильнику количество теплоты Q₂ 0, A > 0, Q₂ T₂

В двигателях, применяемых в технике, используются различные круговые процессы. На рис. 3.11.3 изображены циклы, используемые в бензиновом карбюраторном и в дизельном двигателях. В обоих случаях рабочим телом является смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания состоит из двух изохор (1–2, 3–4) и двух адиабат (2–3, 4–1). Дизельный двигатель внутреннего сгорания работает по циклу, состоящему из двух адиабат (1–2, 3–4), одной изобары (2–3) и одной изохоры (4–1). Реальный коэффициент полезного действия у карбюраторного двигателя порядка 30 %, у дизельного двигателя – порядка 40 %.

Циклы карбюраторного двигателя внутреннего сгорания (1) и дизельного двигателя (2)

В 1824 году французский инженер С. Карно рассмотрел круговой процесс, состоящий из двух изотерм и двух адиабат, который сыграл важную роль в развитии учения о тепловых процессах. Он называется циклом Карно (рис. 3.11.4).

Цикл Карно совершает газ, находящийся в цилиндре под поршнем. На изотермическом участке (1–2) газ приводится в тепловой контакт с горячим тепловым резервуаром (нагревателем), имеющим температуру T₁. Газ изотермически расширяется, совершая работу A₁₂, при этом к газу подводится некоторое количество теплоты Q₁ = A₁₂. Далее на адиабатическом участке (2–3) газ помещается в адиабатическую оболочку и продолжает расширяться в отсутствие теплообмена. На этом участке газ совершает работу A₂₃ > 0. Температура газа при адиабатическом расширении падает до значения T₂. На следующем изотермическом участке (3–4) газ приводится в тепловой контакт с холодным тепловым резервуаром (холодильником) при температуре T₂ 0, T₁ > T₂

Устройство, работающее по холодильному циклу, может иметь двоякое предназначение. Если полезным эффектом является отбор некоторого количества тепла |Q₂| от охлаждаемых тел (например, от продуктов в камере холодильника), то такое устройство является обычным холодильником. Эффективность работы холодильника можно охарактеризовать отношением

т. е. эффективность работы холодильника – это количество тепла, отбираемого от охлаждаемых тел на 1 джоуль затраченной работы. При таком определении β_х может быть и больше, и меньше единицы. Для обращенного цикла Карно

Если полезным эффектом является передача некоторого количества тепла |Q₁| нагреваемым телам (например, воздуху в помещении), то такое устройство называется тепловым насосом. Эффективность β_Т теплового насоса может быть определена как отношение

т. е. количеством теплоты, передаваемым более теплым телам на 1 джоуль затраченной работы. Из первого закона термодинамики следует:

следовательно, β_Т всегда больше единицы. Для обращенного цикла Карно