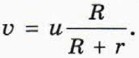Катящееся колесо
Рассмотрим движение различных точек колеса автомобиля.
Пусть автомобиль едет со скоростью 
(рис. 8.10), причём его колёса катятся без проскальзывания.
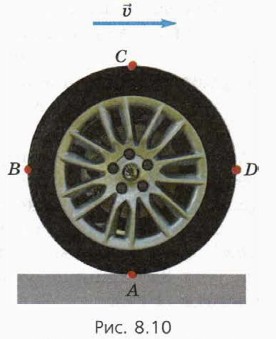
Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют чёткие следы). Этот факт — отправная точка для нахождения скорости всех других точек колеса — например, точек В, С, D на рисунке 8.10.
Чтобы найти скорость этих точек, удобно перейти в систему отсчёта, связанную с автомобилем, а потом вернуться в систему отсчёта, связанную с дорогой.
В системе отсчёта, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим υвр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля и и скорость вращения υвр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.
Заметим, что скорость Авр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).
А = Авр + .
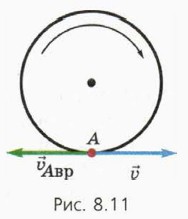
Итак, скорости Авр и направлены противоположно, а их сумма А = 0. Следовательно,
то есть скорость движения точек обода колеса в системе отсчёта, связанной с автомобилем, равна по модулю скорости автомобиля.
15. Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2υ.
16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.
17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью 
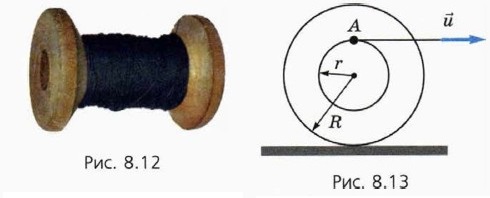
П о д с к а з к а. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.
18. С какой скоростью υ и в каком направлении будет двигаться катушка в случае, изображённом на рисунке 8.14?
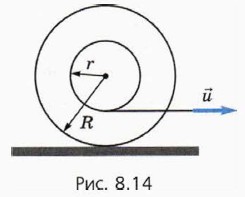
Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.
19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.
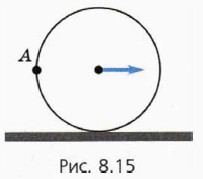
П о д с к а з к а. Перейдите в систему отсчёта, связанную с велосипедистом.
Парадокс колеса
На приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние.
В то же время из школьного курса математики известно, что длина окружности равна:
Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению.
Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен:
C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности.
Но на самом деле она проходит фактически путь вдвое больший.
Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице.
Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле.
Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше.
Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой.
Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]:
V = w*R, где w — угловая скорость вращения колеса.
Фактически линейная скорость внутренних точек колеса должна описываться уравнением:
V = n*w*r, где n = R/r
R – внешний радиус колеса;
r – внутренний радиус.
Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса.
Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил.
Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением:
dV = w*(R-r), где
dV – изменение скорости движения внутренних точек колеса;
R – внешний радиус колеса;
r – внутренний радиус колеса.
При r = R dV = 0
При r = 0 dV = w*R
Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса.
С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость.
Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало.
[1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе.
Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению.
Сазонов Сергей 3 сентября 2019 года в 12:54
Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет.
(конец цитаты)
К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал.
Уничижительное отношение к оппонентам явный признак ограниченной умственной деятельности. Конечно, можно было и не обращать внимание на подобные выпады, но, к сожалению, подобный уровень комментаторов встречается не так уж редко, поэтому считаю необходимым противостоять банальному хамству.
Как определить полный оборот колеса автомобиля
Для начала давайте выясним, для чего нужно уметь определять полный оборот колеса? Знать полный оборот колеса своего авто нужно по разным причинам. В первую очередь, чтобы выяснить периметр колеса (круга).
Это не что иное, как расстояние, которое оно проходит по плоскости за один оборот. Периметр же зависит от диаметра колеса, и здесь уже возможны варианты.
Многие автолюбители устанавливают на машины колеса большего диаметра, чем рекомендует производитель. Зачем это нужно? Многие рассуждают так: чем больше диаметр, тем выше максимальная скорость и короче время разгона, и наоборот. При этом, колесо имеет значительную инерцию, а двигателю сложней его оборачивать.
Нередко водители устанавливают колеса большего размера и для того, чтобы повысить клиренс и сэкономить на топливе, поскольку чем больше колесо, тем длинней пройденный путь.
Если диаметр колеса отличается от стандартного в большую или меньшую сторону, то данные спидометра будут показывать некорректную скорость движения. Так, при меньшем диаметре она будет больше, чем есть на самом деле.
Еще одной причиной знать полный оборот колеса автомобиля является резонансная частота колебаний. Например, за один оборот колесо прошло 2 метра, сильней всего машину трясет на скорости 90 км/ч или 25 м/ч. При таких исходных данных резонансная частота колебаний составит 12,5 Гц.
Как определить длину окружности колеса
Узнать оборот колеса можно двумя способами. Первый самый простой ‒ нанести на боковую часть колеса черту с помощью мела. Она будет выступать своеобразным маячком. Каждое последующее касание этой белой черты дорожного покрытия и будет считаться полным оборотом.
Водители с опытом заверяют, что чувствуют полный оборот на руле. Так, после 2,5 оборотов руль уходит в мертвую точку и перестает крутиться.
Как определить полный оборот колеса по формуле
Определить число оборотов можно и с помощью формулы. Для этого сначала необходимо выяснить длину окружности шины с внешней стороны.
100 000 / С (шины в см).
Пример. Если длина окружности покрышки равна 199,45 см, то рассчитать количество оборотов за километр можно следующим способом:
Число оборотов = 100000 / 199.45 = 501.4 ≈ 501 об./км.
В общем, узнать полный оборот колеса на самом деле не так и сложно. Это позволит уточнить скорость, расстояние и другие технические показатели.
А вы замеряли полный оборот колеса? Как думаете, для чего это нужно и как удобней всего сделать расчет?
