- Шинный калькулятор
- Шинный калькулятор
- Расшифровка параметров шины
- Сравнение шин
- Маркировка шин и расшифровка
- Ширина шины по маркировке
- Как посчитать высоту профиля шины
- Формула
- Пример
- Диаметр диска по маркировке шины
- Диаметр шины по маркировке
- Формула
- Пример
- Длина окружности шины
- Формула
- Пример
- Число оборотов колеса за 1 км
- Формула
- Пример
- Как влияет размер шин на показание спидометра
- Влияние размера шин на клиренс
- Парадокс колеса
- Скорость вращения колеса от скорости автомобиля
Шинный калькулятор
| Старый размер: | / R |
| Новый размер: | / R |
| ||||||||||||||||||||
| ||||||||||||||||||||
Самовывоз шин производится в будние дни с 9.00 до 19.00
Доставка производится в будние дни с 9.00 по 23.00
Вся информация приведенная на сайте дана в качестве справочной и не является публичной офертой.
Введите имя: Введите номер телефона:
Ваш заказ успешно оформлен!
Проверяем наличие товара на складе. Мы свяжемся с вами в ближайшие 10 минут. (в рабочие время)
Шинный калькулятор
Расшифровка параметров шины
| Диаметр шины: |
| Шина №1 эталон | Шина №2 новая шина | Разница | |||
| Диаметр шины: | |||||
| Показания спидометра: | 100 км/ч | 100 км/ч | |||
| Реальная скорость: | В полях «Шина №1» следует указать стандартный типоразмер для вашей машины. Он обычно указан на табличке, наклеенной в проёме водительской двери. В поля «Шина №2» введите параметры шины, которую хотите сравнить с эталоном (с шиной №1). Диаметр нового колеса (шины) не должен отличаться более чем на 3% от диаметра колеса, установленного заводом изготовителем автомобиля. Маркировка шин и расшифровкаШирина шины по маркировкеШирина шины (Wшины) указана первым числом в маркировке в миллиметрах: 225/50 R16 Как посчитать высоту профиля шиныВысота профиля указана в маркировке шины вторым числом в процентах от первого числа (ширины шины): 225/50 R16 Таким образом, чтобы определить её в миллиметрах нужен расчет по следующей формуле: ФормулаHпрофиля в мм = (Wшины ⋅ Hпрофиля в %) / 100 ПримерДля примера посчитаем чему равна высота профиля шины со следующей маркировкой: 205 / 55 R16 Hпрофиля = (205 ⋅ 55) / 100 = 113 мм = 11.3 см Диаметр диска по маркировке шиныОбычно диаметр диска (посадочный диаметр) указан после буквы R (иногда В, D или буква не указана): 225/50 R16. Этот параметр указан в дюймах, поэтому если требуется перевести его в сантиметры, его следует умножить на 2.54. Диаметр шины по маркировкеРасчет диаметра колеса легко произвести, зная диаметр диска и высоту профиля шины. ФормулаПримерДля примера определим диаметр шины в сантиметрах со следующей маркировкой: 205 / 55 R16
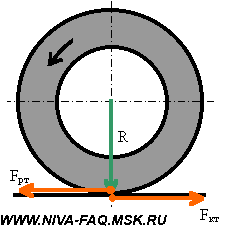
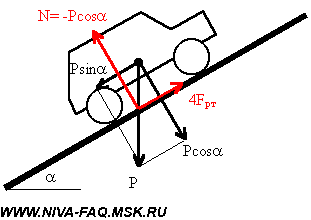
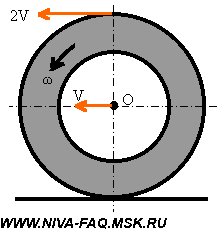
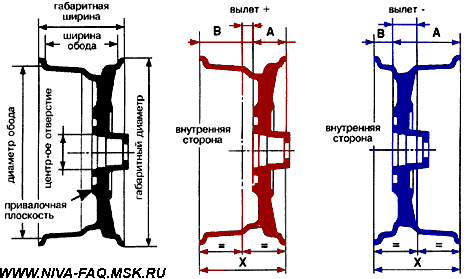
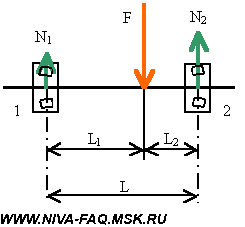
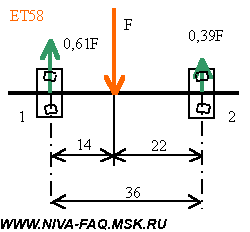
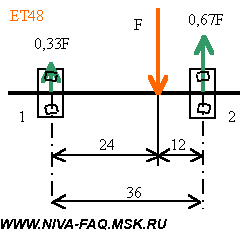
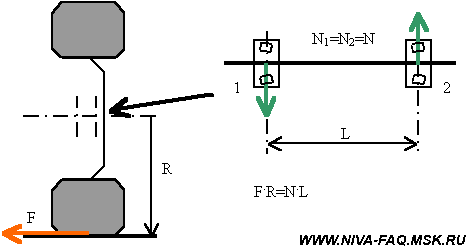
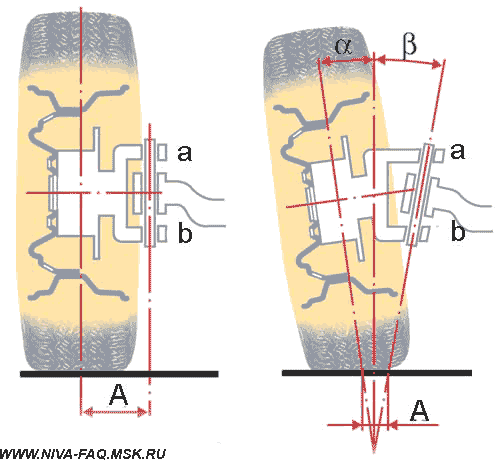
Длина окружности шиныДля того, чтобы рассчитать длину окружности шины Сшины нужно знать её диаметр Dшины. Расчет осуществляется по следующей формуле: ФормулаСшины = π ⋅ Dшины , где π ≈ 3.14 ПримерВозьмём диаметр шины из предыдущего примера Dшины = 63.2 см и определим длину окружности шины с маркировкой: 205 / 55 R16 Сшины = 63.2 ⋅ 3.14 = 198.44 см Число оборотов колеса за 1 кмДля того, чтобы определить число оборотов колеса, при котором оно преодолеет расстояние в один километр, нужно знать длину внешней окружности шины. ФормулаПримерДля колеса с длиной окружности шины 198.44 см посчитаем число оборотов за 1 км: Число оборотов = 100000 / 198.44 = 503.9 ≈ 504 об./км Как влияет размер шин на показание спидометраЕсли диаметр колеса больше или меньше стандартного, то показания спидометра не будут отражать реальную скорость автомобиля. Так, например, если диаметр шины меньше стандартного, то спидометр будет показывать скорость больше, чем она есть на самом деле. И на оборот. Влияние размера шин на клиренсЧем больше диаметр шины, тем больше клиренс. При этом если, например, вы поменяли колесо с диаметром 60 см, на колесо с диаметром 64 см, то клиренс вырос на 2 см. Парадокс колесаНа приведённом рисунке хорошо видно, что все точки расположенные на радиусе колеса при совершении им одного оборота занимают те же самые места, на которых они были до начала вращения. Иными словами все точки радиуса колеса за один оборот перемещаются на одно и то же расстояние. В то же время из школьного курса математики известно, что длина окружности равна: Если прокатить колесо по поверхности и затем замерить пройденный им путь, то он будет точно соответствовать длине его окружности. Таким образом, две точки колеса: центр вращения и точка на внешней окружности проходят путь точно соответствующий приведённому расчёту. Но вот в отношении меньших радиусов мы приходим к выводу, что траектория их движения противоречит каноническому утверждению. Так путь пройденный точкой, расположенной на половине радиуса колеса (r = R/2) должен быть равен: C(r) = пиR, т.е. в половину меньше траектории точки расположенной на внешней окружности. Но на самом деле она проходит фактически путь вдвое больший. Соотношение фактически пройденной траектории и фактической дины окружности описываемый соответствующим радиусом растёт с уменьшением радиуса, фактически до бесконечности. Но в точке вращения он вновь возвращается к единице. Самое удивительное в том, что если вырезать любую внутреннюю часть колеса и измерить его окружность, то она точно будет соответствовать вычисленной по канонической формуле. Рассмотренный парадокс усиливается в случае, если колесо прокатывается с внешней стороны другой окружности. В этом случае траектория внутренних радиусов становится больше траектории точки на внешнем радиусе. И, наоборот, при прокатывании с внутренней стороны их траектория становится меньше. Таким образом, можно сделать вывод о том, что траектория точек расположенных на внутренних радиусах колеса зависти не от величины собственного радиуса, а от радиуса внешней окружности. Что при этом происходит с материальными точками колеса расположенных на этих радиусах в пространстве остаётся загадкой. Единственно разумное объяснение этого феномена предложил Галилей. Он считал, что поскольку фактическая траектория движения внутренних точек значительно больше фактической длины окружности, то точки внутренних радиусов проходят наблюдаемую траекторию с большей скоростью, чем это предписано им физикой [1]: V = w*R, где w — угловая скорость вращения колеса. Фактически линейная скорость внутренних точек колеса должна описываться уравнением: V = n*w*r, где n = R/r Иными словами линейная скорость точек внутренних радиусов является величиной постоянной и зависит только от внешнего радиуса колеса. Вывод прямо скажем обескураживающий, но иного разумного объяснения пока ни кто не предложил. Математически парадокс колеса в интерпретации Галилея описывается следующим уравнением: dV = w*(R-r), где Иными словами, изменение скорости точек расположенных на внутренних радиусах колеса меняется пропорционально от 0 на внешнем радиусе до V=w*R в центре вращения колеса. Поэтому ось колеса перемещается в пространстве с той же скоростью, которая соответствует линейной скорости вращающегося движения внешней окружности колеса при его прямолинейном движении. Соответственно такую же скорость имеют и все внутренние точки колеса. С физической точки зрения полученный результат интерпретируется как движение жёсткого стержня, расположенного перпендикулярно направлению линейного движения оси вращения. Если рассмотреть движение такого стержня без привязки его к вращательному движению, то не трудно заметить, что все материальные точки стержня имеют одну и ту же скорость. Преобразование вращательного движения в линейно-поступательное в данном случае решается методом рычага в рамках курса теоретической механики, которой к сожалению во времена Галилея ещё не существовало. [1] Очевидно, именно по этому, этот парадокс практически не обсуждается в научной литературе. Поскольку один из комментаторов так возбудился после прочтения этой статьи, что внёс меня в свои чёрные списки, и у меня нет возможности ему ответить иным путём, поэтому использую материал статьи не по назначению. Сазонов Сергей 3 сентября 2019 года в 12:54 Писать рецензию на Вашу бредятину «Парадокс колеса» считаю излишним (много чести) — найдите в детском журнале «Квант» за 1975 год статью «ЦИКЛОИДА» . Там — примерно этот круг вопросов. Парадокса нет. К сожалению, найти указанный журнал в Интернете не смог, поэтому не смог лично ознакомиться со статьёй. Но уже само её название «ЦИКЛОИДА» говорит о том, Сергей Сазонов не видит разницы между прямой и циклоидой. В парадоксе колеса траектория меньшего радиуса разворачивается не в виде циклоиды, а в виде прямой линии. В этом то, как раз, и заключается парадокс. С другой стороны, то, что этим парадоксом интересовались Аристотель, Галилей, и возможно другие, не менее, замечательные умы человечества, говорит о том, что парадокс действительно существовал. Скорость вращения колеса от скорости автомобиляКонечно, нельзя, основываясь на школьном курсе физики, обсчитать и описать все поведение автомобиля в меняющихся дорожных условиях. Но некоторые моменты могут быть рассчитаны довольно точно при минимальных упрощениях и допущениях. Просто большинство автолюбителей не задумывается над этим, а если и понимает описанные процессы на интуитивном уровне, то до расчетов у них как правило дело не доходит. Эта статья — попытка простым языком описать некоторые моменты физики взаимодействия автомобиля с дорогой. А тех, кому на первый взгляд в начале изложении все показалось знакомым и примитивным, стоит все-таки просмотреть статью до конца: здесь есть некоторые неочевидные выводы или, по крайней мере, интересные цифры и ссылки. Исходные положения и допущения Приводимые ниже определения вполне сознательно немного упрощены — их нестрогость не повлияет на точность дальнейших рассуждений, но облегчит понимание процессов и закономерностей. Кроме того, будем считать, что в узлах трансмиссии нет трения — оно невелико по сравнению с действующими в них силами. Эти потери будут оценены отдельно. Радиус колеса R для простоты везде и всегда будем считать равным внешнему радиусу покрышки, допуская, что деформация колеса в зоне контакта с дорогой невелика. При расчете размеров колеса удобно пользоваться шинным калькулятором. Для штатной резины Нивы (175/80R16) радиус колеса R=0,343 м. Скорость автомобиля V, ускорение a. Еще нам потребуются угловая скорость вращения колес w =V/R и угловое ускорение e =a/R. Крутящий момент (момент силы) M равен произведению силы F на плечо. В формулах вращательного движения крутящий момент занимает то же место, что и сила при прямолинейном движении. Для нашего случая данного определения вполне достаточно, причем плечо будет равно радиусу колеса R: Передаточное отношение i в механике определяется, как отношение угловых скоростей входного и выходного валов передачи. Применительно к автомобилю угловые скорости принято считать в оборотах в минуту n: Здесь действует так называемое «золотое правило механики»: во сколько раз мы проигрываем в скорости и пути, во столько же раз выигрываем в силе, и соотношение крутящих моментов на валах передачи обратно соотношению скоростей: При нескольких передачах общее передаточное отношение равно произведению передаточных отношений. Сила трения возникает как реакция при попытке смещения одного тела относительно поверхности другого сдвигающей силой, приложенной параллельно этой поверхности. Рассмотрим процесс трения последовательно — по мере роста сдвигающей силы. При небольших значениях сдвигающей силы движению тела препятствует сила трения (реакция поверхности). Она равна приложенной силе, но действует в противоположном направлении. В результате тело остается в покое. По мере роста сдвигающей силы будет расти и сила трения. И это будет продолжаться до тех пор, пока сдвигающая сила не превысит порог Fтр max, после которого тело начнет двигаться. Величину Fтр max определяют через коэффициент трения kт, равный отношению Fтр max к перпендикулярной поверхности прижимающей силе, точнее, равной ей по величине силе реакции N: Обязательно нужно отметить, что при переходе к скольжению сила трения скачком уменьшается. Это знает каждый автомобилист: тормозной путь с заблокированными колесами больше, чем в случае, когда колеса тормозят, но вращаются со скоростью автомобиля «на пределе». Именно поэтому самый короткий тормозной путь обеспечивает система ABS, контролирующая вращение колес при торможении и не позволяющая им заблокироваться. Нас будет интересовать только сила трения между колесом и поверхностью дороги. Коэффициент трения сильно зависит от состояния трущихся поверхностей. Для сухого асфальта коэффициент трения доходит до 0,8, а при наличии пленки воды он падает до 0,1. 0,2, на обледеневшей поверхности — еще меньше. Момент инерции J материальной точки массой m, вращающейся по окружности радиусом r, равен: Ниже нас будет интересовать только момент инерции колеса Jк. Точно рассчитать момент инерции такого сложного по форме тела затруднительно. На основании приближенного расчета, приведенного в Приложении, будем считать, что момент инерции колеса, складывающийся из моментов инерции покрышки (п) и диска (д), определяется формулой: Второй закон Ньютона определяет зависимость между приложенной к телу силой F, массой тела m и ускорением a: Для вращательного движения этот закон имеет вид: Принцип суперпозиции позволяет отдельно рассматривать и рассчитывать составляющие сложного движения. Применительно к настоящей статье будем рассматривать отдельно поступательное движение автомобиля (включая колеса) и вращательное движение колес. Допущением здесь будет то, что мы будем применять принцип суперпозиции в том числе и при ускоренном движении автомобиля. Расчет скорости и крутящего момента Передаточные отношения трансмиссии iт для ВАЗ-21213/214 с пятиступенчатой коробкой передач, двухступенчатой раздаткой и редукторами 3,9 (точнее, 43/11) сведены в таблицу: Передача Чтобы узнать крутящий момент на одном (каждом!) колесе Mк, нужно взять крутящий момент двигателя Mдв, умножить его на значение iт из таблицы и разделить на количество ведущих колес (для Нивы — на четыре). Скорость автомобиля V [км/час] по оборотам двигателя nдв [об/мин] и радиусу колеса R [м] можно рассчитать по формуле: Коэффициент 0,377 учитывает все остальные параметры, включая размерность. Подчеркну, что допущение об отсутствии деформации колеса на точность расчета скорости не влияет: здесь все определяет длина окружности колеса, которая рассчитывается по радиусу как 2 p R. Примечание. Участники конференции vasak и Loggy, которых я попросил посмотреть статью до ее публикации, считают, что деформация колеса в зоне контакта влияет на расчет скорости. В частности, vasak считает , что в формулу следует подставлять радиус нагруженного колеса. Решено провести экспериментальную проверку, результаты которой будут опубликованы. Почему машина едет Парадоксально, но факт: машину «толкает» дорога. Покажем, почему это так. Двигатель создает крутящий момент Mдв. После преобразования трансмиссией этот момент передается на каждое ведущее колесо машины в виде Mк и заставляет колесо вращаться, т. е. создает сдвигающую силу Fкт=Mк/R в точке контакта колеса с дорогой, причем эта сила через колесо приложена к дороге. Поверхность дороги препятствует вращению колеса силой трения Fрт той же величины, но приложенной к колесу и направленной противоположно. Чтобы показать, что силы действуют на разные объекты, точки приложения сил на рисунке условно немного разнесены по вертикали: Эта сила реакции трения Fрт, умноженная на число ведущих колес, и движет машину. Применительно к Ниве разгоняющим усилием будет величина 4Fрт. Определим эту величину. Максимальный крутящий момент Mдв=127 Н . м двигатель ВАЗ-21213 развивает при 3200-3400 об/мин (это паспортные данные двигателя 1,7). Значит, на первой передаче в КПП при пониженной в раздатке суммарный крутящий момент на колесах будет равен: При колесах штатного размера тяговое усилие всех четырех колес составит: При нормальной передаче в раздатке сила станет в 1,78 раза меньше и будет уменьшаться дальше при повышении передач в КПП. При тех же оборотах двигателя на пятой передаче тяговое усилие составит всего 152 кГ. В узлах трансмиссии неизбежно существует трение. Согласно «Деталям машин» Д. Н. Решетова КПД закрытой среднескоростной цилиндрической одноступенчатой зубчатой передачи составляет около 98%, конической — около 97%. В коробке передач мы имеет две ступени (от первичного вала к промежуточному и от промежуточного к вторичному). Аналогично — две ступени в раздатке. Все эти передачи — цилиндрические. А в мостах — гипоидные передачи, близкие к коническим. Поэтому КПД трансмиссии будет приблизительно равен: К этому добавятся еще потери на трение в карданах, ШРУСах и подшипниках. Поэтому из-за трения в узлах трансмиссии реальные значения усилий будут примерно на 10-15% меньше рассчитанных. Вспомним о силе трения и коэффициенте трения между колесом и поверхностью дороги. Если Fкт=Mк/R меньше максимальной силы трения Fрт max, машина будет нормально разгоняться силой 4Fрт. Если же Mк/R>Fрт max, то избыток крутящего момента пойдет просто на раскручивание ведущих колес — они начнут буксовать. На заснеженном или обледеневшем асфальте часто можно наблюдать такое у моноприводных машин, иногда они даже не могут тронуться с места. Поскольку у Нивы крутящий момент распределен на четыре колеса, каждая из сил Fрт оказывается вдвое меньше, чем у машин с неполным приводом, а максимальная сила трения примерно такая же. Это дает значительное преимущество Ниве при разгоне на зимней дороге. Но не нужно забывать, что тормозят и моноприводные машины, и Нива — всеми четырьмя колесами. О силах, противодействующих разгону автомобиля на горизонтальной дороге, можно почитать статьи, скопированные с сайта http://autotheory.by.ru: «Момент сопротивления качению» и «Аэродинамическое сопротивление автомобиля». Особое внимание обратим на последний фактор — сопротивление воздуха растет пропорционально квадрату скорости и после 100 км/час на горизонтальном участке дороги оно превышает все иные противодействующие движению силы, взятые вместе. В результате именно сопротивление воздуха определяет максимальную скорость автомобиля. Подробнее о максимальной скорости будет сказано в конце статьи. Рассмотрим силы, действующие на автомобиль на наклонной плоскости с углом a к горизонту: Вес автомобиля P можно разложить на две составляющие. Первая (Psin a ) — скатывающая сила — направлена параллельно поверхности и противодействует подъему автомобиля, ее и должно преодолеть тяговое усилие 4Fрт, чтобы машина взяла подъем. Вторая (Pcos a ), направленная перпендикулярно дороге, прижимает колеса к поверхности и обеспечивает их трение о дорогу и силу реакции N=-Pcos a . На рисунке показаны равнодействующие сил реакции и трения всех четырех колес. Хочу подчеркнуть, что прижимающая сила стала меньше на величину cos a , т. е. по сравнению с горизонтальным участком дороги предельная сила трения стала меньше: Расчет тягового усилия (максимум 1155 кГ) хорошо согласуется с паспортными данными Нивы о преодолеваемом уклоне 58% (tg30 о =0,58). Разрешенная максимальная масса ВАЗ-21312 равна 1870 кг, sin30 о =0,5, значит, тяговое усилие должно быть не меньше 1870 . 0,5=935 кГ. Подъем будет взят только в том случае, если сцепление колес с дорогой окажется достаточным для обеспечения такой силы тяги при прижимающем усилии, составляющем 87% веса машины (cos30 o =0,87). При дальнейшем увеличении крутизны подъема скатывающая сила будет расти, а прижимающая сила и предельная сила трения — уменьшаться. Важное замечание. Преобразование крутящего момента в трансмиссии сопровождается образованием внутренних реактивных сил в узлах трансмиссии, причем эти силы тем больше, чем бОльший крутящий момент ею передается. Превышение некоторого порога может привести к разрушению элементов трансмиссии, в чем автор имел неосторожность убедиться на собственном опыте. При попытке штурма довольно крутого подъема в Крылатском машине не хватало сцепления с почвой, и колеса буксовали. Чтобы улучшить сцепление, на колеса передней оси были одеты цепи и включена блокирвка дифференциала в раздатке. Все это привело к существенному возрастанию момента на передних колесах и вывело из строя редуктор переднего моста: подшипник ведущего вала РПМ выдавило вместе с куском стенки картера размером 10х10 см. Напомню, что при заблокированной раздатке крутящий момент в ней направляется в сторону наибольшего сопротивления вращению (см. статью Привод Нивы), т. е. в сторону переднего моста, где цепи обеспечивали хорошее сцепление с почвой. Цепи — «лесенки», образованные поперечными цепными перемычками с интервалом около 25 см. Поэтому колесо проворачивалось рывками с проскальзыванием в промежутках между цепными перемычками, т. е. возникала ударная нагрузка. Во время одного из рывков реактивная сила, передаваемая подшипником ведущего вала на стенку РПМ, превысила предел прочности стенки. Разгон и торможение По второму закону Ньютона суммарная сила Fрт всех ведущих колес разгоняет автомашину массой mа с ускорением a. Но часть крутящего момента расходуется на раскручивание колес. Рассмотрим этот вопрос подробнее. По принципу суперпозиции движение колеса можно рассматривать как сумму двух движений: прямолинейное вместе со всей машиной со скоростью V и вращение вокруг оси: Если колесо не проскальзывает относительно поверхности (нет заноса), мгновенная скорость в зоне контакта (самой нижней точке колеса) должна быть равна нулю — там прямолинейная скорость движения машины (и оси колеса) V компенсируется такой же по величине, но противоположно направленной скоростью вращения назад. А в самой верхней точке скорость вращения колеса складывается с прямолинейной скоростью и оказывается равной 2V. При таком вращении угловая скорость колеса равна w =V/R. При равномерном движении ускорение автомобиля a и угловое ускорение колеса e равны нулю. Весь момент 4Mк идет на создание тягового усилия 4Fрт=4Mк/R и преодоление сопротивления движению автомобиля. Но на этапе разгона, когда ускорение a>0, помимо разгона автомобиля массой mа нужно еще обеспечить колесам с моментом инерции Jк угловое ускорение e =a/R>0 . Поэтому Fрт . R+4Jк . e =mа . a . R+4Jк . a/R. Здесь большая часть момента (первое слагаемое) разгоняет автомобиль силой 4Fрт, а второе слагаемое — раскручивает колеса. Если разделить второй член суммы на первый, мы получим долю момента, приходящуюся на раскручивание колес: Масса штатного колесного диска 16″ mд=9,3 кг (данные Nivandy), масса штатной покрышки ВлИ-10 с камерой mп=12 кг. Тогда: Jк=0,78mдRд 2 +0.85mпR 2 =0,78 . 9,3 . 0,203 2 +0,85 . 12 . 0,343 2 =0,30+1,20=1,50 кг . м 2 . Массу Нивы с одним водителем примем равной mа=1300 кг. Тогда: Итак, доля крутящего момента, расходуемая на раскрутку колес штатного размера, равна 3,9%. В дальнейшем эта цифра нам пригодится. Строго говоря, раскрутить нужно не только колеса, но и все вращающиеся элементы трансмиссии. Но доля колес в общем моменте инерции вращающихся деталей на один-два порядка больше, чем у любой другой вращающейся детали трансмиссии. Поэтому их вращением будем пренебрегать. Процессы при торможении аналогичны разгону, только колеса затормаживаются тормозными колодками, которые создают момент, противодействующий вращению колес. Этот момент тоже делится на две неравные части. На снижение скорости движения автомобиля расходуется та часть момента, за счет которой колеса тормозятся о поверхность дороги. Но часть тормозного момента пойдет на снижение скорости вращения колес. И чем больше момент инерции колес, тем меньшая часть момента пойдет на снижение скорости собственно автомобиля. Колесо стало больше Пусть на Ниву вместо колес штатного размера поставили колесо бОльшего диаметра, например, Я-569 (235/75R15). Как это сделать (проставки под шаровые, резка арок и проч.) — не является предметом настоящей статьи. Нас интересует, как изменится динамика машины, и под этим мы будем понимать изменение ускорения при разгоне машины. Радиус Я-569 0,369 м, т. е. дорожный просвет (клиренс) увеличится на 369-343=26 мм (примерно на дюйм). Посчитаем, чем придется заплатить за это повышение проходимости. Радиус колеса увеличился относительно штатного размера колеса на 7,6%. Это означает, что при прежнем крутящем моменте на колесе Mк из-за увеличения радиуса R силы Fкт=Fрт=Mк/R будут меньше на 7.6%, т. е. динамика машины будет хуже. Общая масса автомобиля возросла на величину: Из-за этого масса автомобиля стала равной mа=1300+50,8=1350,8 кг, т. е. больше на 50,8/1300=3,9%. Из-за этого при прежней силе Fрт ускорение a=Fрт/mа уменьшится на те же 3,9%. А теперь определим влияние момента инерции этих колес. Масса бескамерной покрышки Я-569 20 кг. Масса штампованного диска 15″ от УАЗа около 14 кг (данные Nivandy). Считаем: Jк=0,78mдRд 2 +0,85mпR 2 =0,78 . 14 . 0,19 2 +0,85 . 20 . 0,369 2 =0,39+2,31=2,70 кг . м 2 Доля крутящего момента, расходуемого на раскрутку колес: 4Jк/mа . R 2 =4 . 2,70/1350,8 . 0,369 2 =0,059=5,9%. Вспомним, что при штатных колесах на их раскрутку тратилось 3,9% крутящего момента. Из-за необходимости раскрутить более массивные колеса на разгон автомобиля пойдет часть момента еще на 2,0% меньшая. Посчитаем общее ухудшение динамики при установке колес большого диаметра: 1,076 . 1,039 . 1,020=1,140. Итого из-за установки колес Я-569 на дисках от УАЗа динамика ухудшается на 14,0%. Нива была создана как компромисс между шоссейным автомобилем и вездеходом. Она имеет вполне приличную динамику и скорость, позволяющую ей ехать по шоссе, практически ни в чем не уступая другим легковым автомобилям. И вместе с тем у Нивы вполне приличная проходимость вне асфальта. Колеса большого диаметра нарушают этот компромисс в сторону внедорожности. Впрочем, крутизна преодолеваемого подъема также уменьшится. Возникает вопрос: как сохранить динамику? В формуле, связывающей крутящий момент, радиус колеса и силу, мы пока изменили только один член — радиус. Чтобы сохранить динамику прежней, нужно увеличить крутящий момент на колесах. Это означает, что нужно либо поставить двигатель с бОльшим крутящим моментом (дорого, да и выбор мал), либо переделать трансмиссию так, чтобы при том же моменте двигателя момент на колесах стал больше, т. е. изменить ее передаточное отношение. КПП для Нивы выпускается только с одним набором передаточных отношений, раздатка — тоже. Остается одновременная замена редукторов переднего и заднего моста, и этот выбор не так уж и мал. Производятся серийно и есть в обычных магазинах запчастей передние и задние редукторы с передаточными отношениями 3,9, 4,1 и 4,3 (подробности — в соответствующих статьях FAQ: здесь и здесь). Ранее выпускались редукторы 2102 (передаточное отношение 4,44). Существуют тюнинговые главные пары редукторов с передаточными отношениями 5,25 и др. Штатно в 21213/214 ставятся редукторы с передаточным отношением 3,9 (точнее, 43/11=3,91). Если поменять их на редукторы 4,1, момент на колесах вырастет на 4,9%, а если на 4,3 — то на 10%. Но даже в последнем случае при резине Я-569 динамика все-таки будет хуже, чем на резине штатного размера. Немного улучшить положение могут легкосплавные диски с меньшей массой. Но выигрыш не так велик, как хотелось бы. Для иллюстрации по той же методике пересчитаем изменение динамики (относительно штатных колес) для Я-569 на легкосплавных дисках «Эллада» с массой 5,2 кг. Радиус покрышки тот же, что и в предыдущем расчете, поэтому Fкт=Fрт=Mк/R будут меньше на 7.6%, чем при штатных колесах. Общая масса машины (опять относительно штатных колес) увеличилась на: Из-за этого при прежней силе Fрт ускорение a уменьшится на 15,6/1300=1,2%. Момент инерции колеса: Jк=0,78mдRд 2 +0,85mпR 2 =0,78 . 5,2 . 0,19 2 +0,85 . 20 . 0,369 2 =0,15+2,31=2,46 кг . м 2 . Доля крутящего момента, расходуемого на раскрутку колес: 4Jк/mа . R 2 =4 . 2,46/1315,6 . 0,369 2 =0,055=5,5%. Относительно 3,9% для штатных колес проигрыш 1,6%. Общее ухудшение динамики: 1,076 . 1,012 . 1,016=1,106. Следовательно, при Я-569 на легкосплавных дисках динамика ухудшится на 10,6%. Колеса 14″, вылет и плечо обката Есть такие любители уродовать Ниву — они ставят на на нее волговские колеса 14 дюймов с нулевым вылетом. Клиренс, разумеется, будет меньше, но динамика машины вырастет: при меньшем радиусе R и прежнем моменте Mк сила Fкт=Fрт=Mк/R станет больше. К тому же уменьшится масса и момент инерции колес. Но в этом параграфе речь будет идти не о динамике, а о влиянии вылета колесных дисков на нагрузку ступичных подшипников и плечо обката. Взаимодействие ступицы с колесом удобно представить силой, лежащей в плоскости симметрии колеса (т. е. в средней плоскости колеса). Вылет — расстояние между этой плоскостью симметрии и посадочной плоскостью, где диск крепится к ступице. Иллюстрирующий это рисунок взят с сайта http://www.protcar.com: У штатного диска Нивы положительный вылет колеса, равный 58 мм (ЕТ58), он соответствует среднему рисунку. Сначала заметим, что устойчивость машины на дороге в значительной степени определяется величиной отношения ширины колеи к колесной базе (расстоянию между осями). Колесные диски с нулевым вылетом расширят колею на 58 . 2= 116 мм, что заметно ухудшит устойчивость Нивы. А теперь разберемся с нагрузкой на ступичные подшипники. Мнение, что из-за слишком малого вылета волговских дисков подшипники приходится менять буквально на каждом ТО, в конференции существует давно. Обоснуем это утверждение. Вспомним, как устроена ступица переднего колеса Нивы (посмотреть это можно в иллюстрированном альбоме). Нагрузку F, действующую в плоскости симметрии колеса, принимают на себя два упорных роликовых подшипника, в которых возникают силы реакции N1 и N2. Эти силы и определяют степень нагруженности подшипников: Нагрузка F — это равнодействующая всех сил, действующих на колесо в продольной плоскости, т. е. не только вес машины, приходящийся на колесо, но и всевозможные удары при наезде на препятствия, кочки и выбоины, причем эти удары могут создавать нагрузку, на порядок большую, чем вес. В зависимости от точки приложения силы F относительно подшипников силы N1 и N2 меняются. В принципе, подобный объект — балка на двух опорах — является предметом курса «Сопротивление материалов», но вывод расчетных формул очень прост. Достаточно применить познания из курса элементарной физики и рассматривать балку как рычаг. Принимаем за точку опоры рычага подшипник 1. Поскольку рычаг неподвижен, моменты сил F и N2 должны уравновешивать друг друга: Можно составить такое же уравнение для определения N1, но удобнее использовать тот факт, что сила F в точности уравновешивается реактивными силами (результат будет тот же): С реальных запчастей были сняты размеры. Оказалось, что расстояние между подшипниками (по серединам) составляет 36 мм, а при штатном диске точка приложения силы F оказывается на 4 мм глубже середины расстояния между подшипниками. При штатном диске нагрузка делится между подшипниками следующим образом: Для штампованных стальных (ЕТ48) и легкосплавных (ЕТ40) дисков Шеви-Нивы:
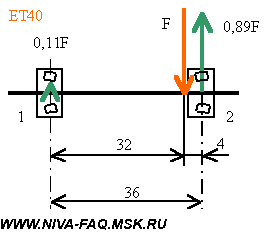
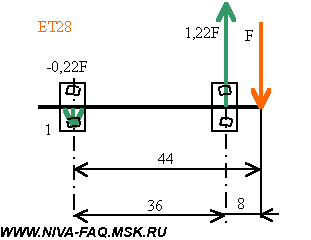
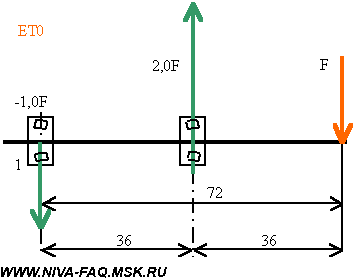
Для легкосплавных дисков «Нива» (ВСМПО, ЕТ28) и волговских дисков (ЕТ0):
Обратите внимание, что при вылетах меньше 36 мм нагрузка внутреннего (левого на рисунках) подшипника меняет знак, а на внешнем (правом) становится больше приложенной силы F. Получается, что при дисках с нулевым вылетом нагрузка внешнего подшипника ступицы в 5,1 раза больше, чем при штатном диске. Если за отправную точку взять нагрузку внутреннего подшипника при штатном диске, это превышение составит 3,3 раза. Отсюда и скорый выход из строя внешнего ступичного подшипника. При поворотах автомобиля возникает боковое усилие на колесах, которое порождает крутящий момент в вертикальной плоскости, проходящей через ось оси ступицы. Момент уравновешивается парой сил реакции на ступичных подшипниках: Величина этих сил определяется соотношением между радиусом колеса R и расстоянием между подшипниками L и от значения вылета не зависит: F . R=N . L; N=F . R/L. Для штатного размера колес отношение R/L=343/36=9,53, т. е. нагрузка подшипников в повороте примерно в 10 раз больше бокового усилия на колесе. На крутых поворотах это тонны. А теперь вспомним, что такое плечо обката. Очень хорошо это иллюстрирует рисунок с сайта журнала «За рулем»: Центр зоны контакта колеса с дорогой (левые оси на рисунках) смещен относительно оси поворота колеса (правые оси, проходящие через шаровые опоры a и b) на величину плеча обката А. Поэтому для поворота колеса нужно преодолеть момент силы трения Mт=Fт . A. При увеличении плеча обката пропорционально будет расти и этот момент. Вот данные Сергея Мишина о плече обката Нивы и Шеви-Нивы: |