Физика
Второе начало термодинамики возникло из анализа работы тепловых двигателей (машин). В формулировке Кельвина оно выглядит следующим образом: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.
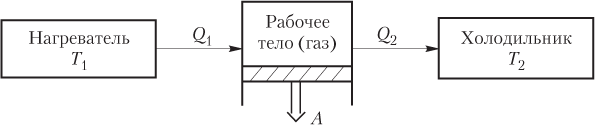
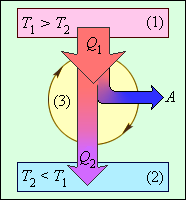
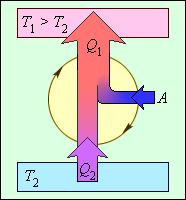
Схема действия тепловой машины (теплового двигателя) представлена на рис. 6.3.
Цикл работы теплового двигателя состоит из трех этапов:
1) нагреватель передает газу количество теплоты Q 1 ;
2) газ, расширяясь, совершает работу A ;
3) для возвращения газа в исходное состояние холодильнику передается теплота Q 2 .
Из первого закона термодинамики для циклического процесса
где Q — количество теплоты, полученное газом за цикл, Q = Q 1 − Q 2 ; Q 1 — количество теплоты, переданное газу от нагревателя; Q 2 — количество теплоты, отданное газом холодильнику.
Поэтому для идеальной тепловой машины справедливо равенство
Когда потери энергии (за счет трения и рассеяния ее в окружающую среду) отсутствуют, при работе тепловых машин выполняется закон сохранения энергии
где Q 1 — теплота, переданная от нагревателя рабочему телу (газу); A — работа, совершенная газом; Q 2 — теплота, переданная газом холодильнику.
Коэффициент полезного действия тепловой машины вычисляется по одной из формул:
η = A Q 1 ⋅ 100 % , η = Q 1 − Q 2 Q 1 ⋅ 100 % , η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,
где A — работа, совершенная газом; Q 1 — теплота, переданная от нагревателя рабочему телу (газу); Q 2 — теплота, переданная газом холодильнику.
Наиболее часто в тепловых машинах используется цикл Карно , так как он является самым экономичным.
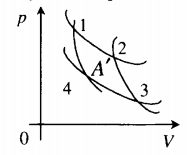
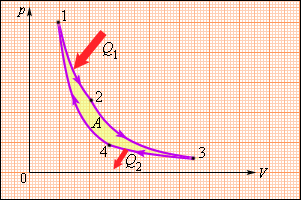
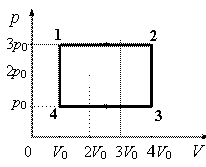
Цикл Карно состоит из двух изотерм и двух адиабат, показанных на рис. 6.4.
Участок 1–2 соответствует контакту рабочего вещества (газа) с нагревателем. При этом нагреватель передает газу теплоту Q 1 и происходит изотермическое расширение газа при температуре нагревателя T 1 . Газ совершает положительную работу ( A 12 > 0), его внутренняя энергия не изменяется (∆ U 12 = 0).
Участок 2–3 соответствует адиабатному расширению газа. При этом теплообмена с внешней средой не происходит, совершаемая положительная работа A 23 приводит к уменьшению внутренней энергии газа: ∆ U 23 = − A 23 , газ охлаждается до температуры холодильника T 2 .
Участок 3–4 соответствует контакту рабочего вещества (газа) с холодильником. При этом холодильнику от газа поступает теплота Q 2 и происходит изотермическое сжатие газа при температуре холодильника T 2 . Газ совершает отрицательную работу ( A 34 U 34 = 0).
Участок 4–1 соответствует адиабатному сжатию газа. При этом теплообмена с внешней средой не происходит, совершаемая отрицательная работа A 41 приводит к увеличению внутренней энергии газа: ∆ U 41 = − A 41 , газ нагревается до температуры нагревателя T 1 , т.е. возвращается в исходное состояние.
Коэффициент полезного действия тепловой машины, работающей по циклу Карно, вычисляется по одной из формул:
η = T 1 − T 2 T 1 ⋅ 100 % , η = ( 1 − T 2 T 1 ) ⋅ 100 % ,
где T 1 — температура нагревателя; T 2 — температура холодильника.
Пример 9. Идеальная тепловая машина совершает за цикл работу 400 Дж. Какое количество теплоты передается при этом холодильнику, если коэффициент полезного действия машины равен 40 %?
Решение . Коэффициент полезного действия тепловой машины определяется формулой
где A — работа, совершаемая газом за цикл; Q 1 — количество теплоты, которое передается от нагревателя рабочему телу (газу).
Искомой величиной является количество теплоты Q 2 , переданное от рабочего тела (газа) холодильнику, не входящее в записанную формулу.
Связь между работой A , теплотой Q 1 , переданной от нагревателя газу, и искомой величиной Q 2 устанавливается с помощью закона сохранения энергии для идеальной тепловой машины
Уравнения образуют систему
η = A Q 1 ⋅ 100 % , Q 1 = A + Q 2 , >
которую необходимо решить относительно Q 2 .
Для этого исключим из системы Q 1 , выразив из каждого уравнения
Q 1 = A η ⋅ 100 % , Q 1 = A + Q 2 >
и записав равенство правых частей полученных выражений:
A η ⋅ 100 % = A + Q 2 .
Искомая величина определяется равенством
Q 2 = A η ⋅ 100 % − A = A ( 100 % η − 1 ) .
Расчет дает значение:
Q 2 = 400 ⋅ ( 100 % 40 % − 1 ) = 600 Дж.
Количество теплоты, переданной за цикл от газа холодильнику идеальной тепловой машины, составляет 600 Дж.
Пример 10. В идеальной тепловой машине от нагревателя к газу поступает 122 кДж/мин, а от газа холодильнику передается 30,5 кДж/мин. Вычислить коэффициент полезного действия данной идеальной тепловой машины.
Решение . Для расчета коэффициента полезного действия воспользуемся формулой
η = ( 1 − Q 2 Q 1 ) ⋅ 100 % ,
где Q 2 — количество теплоты, которое передается за цикл от газа холодильнику; Q 1 — количество теплоты, которое передается за цикл от нагревателя рабочему телу (газу).
Преобразуем формулу, выполнив деление числителя и знаменателя дроби на время t :
η = ( 1 − Q 2 / t Q 1 / t ) ⋅ 100 % ,
где Q 2 / t — скорость передачи теплоты от газа холодильнику (количество теплоты, которое передается газом холодильнику в секунду); Q 1 / t — скорость передачи теплоты от нагревателя рабочему телу (количество теплоты, которое передается от нагревателя газу в секунду).
В условии задачи скорость передачи теплоты задана в джоулях в минуту; переведем ее в джоули в секунду:
Q 1 t = 122 кДж/мин = 122 ⋅ 10 3 60 Дж/с ;
Q 2 t = 30,5 кДж/мин = 30,5 ⋅ 10 3 60 Дж/с .
Рассчитаем коэффициент полезного действия данной идеальной тепловой машины:
η = ( 1 − 30,5 ⋅ 10 3 60 ⋅ 60 122 ⋅ 10 3 ) ⋅ 100 % = 75 % .
Пример 11. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, равен 25 %. Во сколько раз увеличится коэффициент полезного действия, если температуру нагревателя увеличить, а температуру холодильника уменьшить на 20 %?
Решение . Коэффициент полезного действия идеальной тепловой машины, работающей по циклу Карно, определяется следующими формулами:
- до изменения температур нагревателя и холодильника —
η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % ,
где T 1 — первоначальная температура нагревателя; T 2 — первоначальная температура холодильника;
- после изменения температур нагревателя и холодильника —
η 2 = ( 1 − T ′ 2 T ′ 1 ) ⋅ 100 % ,
где T ′ 1 — новая температура нагревателя, T ′ 1 = 1,2 T 1 ; T ′ 2 — новая температура холодильника, T ′ 2 = 0,8 T 2 .
Уравнения для коэффициентов полезного действия образуют систему
η 1 = ( 1 − T 2 T 1 ) ⋅ 100 % , η 2 = ( 1 − 0,8 T 2 1,2 T 1 ) ⋅ 100 % , >
которую необходимо решить относительно η 2 .
Из первого уравнения системы с учетом значения η 1 = 25 % найдем отношение температур
T 2 T 1 = 1 − η 1 100 % = 1 − 25 % 100 % = 0,75
и подставим во второе уравнение
η 2 = ( 1 − 0,8 1,2 ⋅ 0,75 ) ⋅ 100 % = 50 % .
Искомое отношение коэффициентов полезного действия равно:
η 2 η 1 = 50 % 25 % = 2,0 .
Следовательно, указанное изменение температур нагревателя и холодильника тепловой машины приведет к увеличению коэффициента полезного действия в 2 раза.
Тепловые машины и второе начало термодинамики
теория по физике 🧲 термодинамика
Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику.
Второе начало термодинамики
В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.
В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры.
На графике цикл Карно представляется как две адиабаты и две изотермы:
- 1–2 — изотермическое расширение;
- 2–3 — адиабатное расширение;
- 3–4 — изотермическое сжатие;
- 4–1 — адиабатное сжатие.
КПД тепловой машины
Максимальный КПД соответствует циклу Карно.
Второе начало термодинамики
η = Q н − Q х Q н . . 100 % = Q н − P х t Q н . . 100 %
Преобразовывая формулу, получим:
η = A ‘ Q н . . 100 %
η = N t Q н . . 100 %
η = A ‘ A ‘ + Q х . . 100 %
η = T н − T х T н . . 100 %
- Qн (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
- Qх (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
- A’ (Дж) — работа, совершенная газом;
- N (Вт) — полезная мощность;
- t (с) — время;
- Tн (К) — температура нагревателя;
- Tх (К) — температура холодильника.
Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.
Алгоритм решения задач на определение КПД теплового процесса
Рассмотрим решение на примере конкретной задачи:
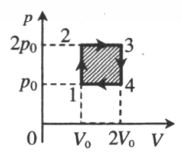
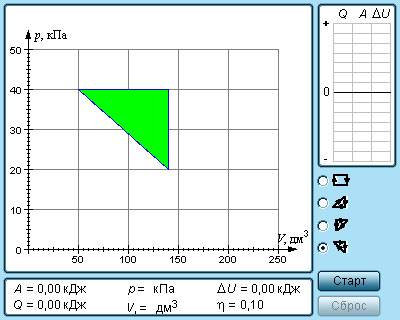
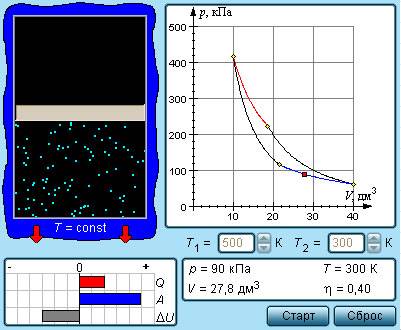
На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.
Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:
Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.
- Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:
1–2: V = const, давление увеличивается, температура увеличивается.
2–3: p = const, объем увеличивается, температура увеличивается.
3–4: V = const, давление понижается, температура понижается.
4–1: p = const, объем уменьшается, температура уменьшается.
Отсюда следует, что газ получает энергию только на первом и втором этапах.
- Определить с помощью первого начала термодинамики количество теплоты, полученное газом:
Q 12 = Δ U 12 = 3 2 . . Δ p V = 3 2 . . Δ p 0 V 0 = 1 , 5 p 0 V 0
Δ U 23 = Q 23 − A 23 ;
Δ U 23 = 3 2 . . Δ p V = 3 2 . . 2 Δ p 0 V 0 = 3 p 0 V 0
A 23 = p Δ V = 2 p 0 V 0
Q 23 = 3 p 0 V 0 + 2 p 0 V 0 = 5 p 0 V 0
Общее количество теплоты:
Q п о л у ч = Q 12 + Q 23 = 6 , 5 p 0 V 0
- Вычислить КПД, используя основную формулу:
η = A ‘ Q п о л у ч . . 100 %
η = p 0 V 0 6 , 5 p 0 V 0 . . 100 % = 15 , 4 %
Тепловые двигатели. Термодинамические циклы. Цикл Карно
Устройство, имеющее способность преобразовывать полученную теплоту в механическую работу носит название теплового двигателя. В таких машинах механическая работа совершается в процессе расширения вещества, называющегося рабочим телом. Его роль обычно исполняют газообразные вещества, вроде паров бензина, воздуха и водяного пара.
Рабочее тело приобретает или отдает тепловую энергию при теплообмене с телами, которые имеют внушительный запас внутренней энергии. Такие тела называют тепловыми резервуарами.
Исходя из первого закона термодинамики, можно сделать вывод, что полученное газом количество теплоты Q полностью преобразуется в работу A в условиях изотермического процесса, при котором внутренняя энергия не претерпевает изменений ( Δ U = 0 ) :
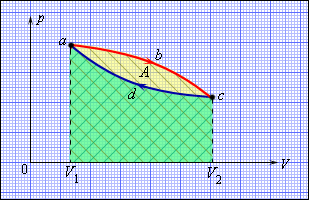
Однако, подобный однократный акт превращения теплоты в работу для техники не представляет интереса. Существующие тепловые двигатели, такие как паровые машины, двигатели внутреннего сгорания и им подобные, работают циклически. Необходимо периодическое повторение процесса теплопередачи и преобразования полученной теплоты в работу. Чтобы данное условие выполнялось, рабочее тело должно совершать круговой процесс или же термодинамический цикл, при котором исходное состояние с периодически восстанавливается. На рисунке 3 . 11 . 1 в виде диаграммы ( p , V ) газообразного рабочего тела с помощью замкнутых кривых проиллюстрированы круговые. В условиях расширения газ производит положительную работу A 1 , эквивалентную площади под кривой a b c . При сжатии газ совершает отрицательную работу A 2 , равную по модулю площади под кривой c d a . Полная работа за цикл A = A 1 + A 2 на диаграмме ( p , V ) равняется площади цикла. Работа A положительна, в том случае, если цикл проходит по часовой стрелке, и A отрицательна, когда цикл проходит в противоположном направлении.
Рисунок 3 . 11 . 1 . Круговой процесс на диаграмме ( p , V ) . a b c – кривая расширения, c d a – кривая сжатия. Работа A в круговом процессе равна площади фигуры a b c d .
Все круговые процессы обладают общей чертой. Они не могут привестись в действие при контакте рабочего тела только с одним тепловым. Их минимальное число должно быть равным двум.
Тепловой резервуар, обладающий более высоким значением температуры, носит название нагревателя, а с более низким – холодильника.
Рабочее тело при совершении кругового процесса получает от нагревателя некоторую теплоту Q 1 > 0 и теряет, отдавая холодильнику, количество теплоты Q 2 0 . Для полного полученного рабочим телом за цикл количества теплоты Q справедливо следующее выражение:
Q = Q 1 + Q 2 = Q 1 — Q 2 .
Совершая цикл, рабочее тело приходит в свое первоначальное состояние, из чего можно сделать вывод, что изменение его внутренней энергии равняется Δ U = 0 . Основываясь на первом законе термодинамики, запишем:
Из этого следует:
Работа A , которую рабочее тело совершает за цикл, эквивалентна полученному за этот же цикл количеству теплоты Q .
Коэффициентом полезного действия или же КПД η теплового двигателя называют отношение работы A к полученному рабочим телом за цикл от нагревателя количеству теплоты Q 1 , то есть:
η = A Q 1 = Q 1 — Q 2 Q 1 .
Рисунок 3 . 11 . 2 . Модель термодинамических циклов.
Коэффициент полезного действия теплового двигателя демонстрирует, какая доля тепловой энергии, которую получило рабочее тело от нагревателя, преобразовалась в полезную работу. Оставшаяся часть ( 1 – η ) была без пользы передана холодильнику. Коэффициент полезного действия тепловой машины не может быть больше единицы η 1 . На рисунке 3 . 11 . 3 проиллюстрирована энергетическая схема тепловой машины.
Рисунок 3 . 11 . 3 . Энергетическая схема тепловой машины: 1 – нагреватель; 2 – холодильник; 3 – рабочее тело, совершающее круговой процесс. Q 1 > 0 , A > 0 , Q 2 0 ; T 1 > T 2 .
Виды тепловых двигателей
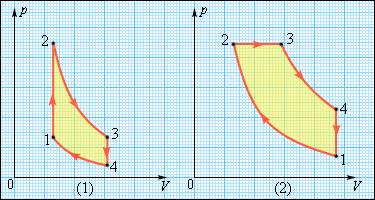
В технике свое применение находят двигатели, использующие круговые процессы. Рисунок 3 . 11 . 3 демонстрирует нам циклы, применяемые в бензиновом карбюраторном и в дизельном двигателях. Они оба в качестве рабочего тела используют смесь паров бензина или дизельного топлива с воздухом. Цикл карбюраторного двигателя внутреннего сгорания включает в себя две изохоры ( 1 – 2 , 3 – 4 ) и две адиабаты ( 2 – 3 , 4 – 1 ) , дизельного двигателя -две адиабаты ( 1 – 2 , 3 – 4 ) , одну изобару ( 2 – 3 ) и одну изохору ( 4 – 1 ) . Реальный КПД (коэффициент полезного действия) у карбюраторного двигателя составляет около 30 % , у дизельного двигателя – приблизительно 40 % .
Рисунок 3 . 11 . 4 . Циклы карбюраторного двигателя внутреннего сгорания ( 1 ) и дизельного двигателя ( 2 ) .
Цикл Карно
Круговой процесс, изображенный на рисунке 3 . 11 . 5 , состоящий из двух изотерм и двух адиабат был назван циклом Карно в честь открывшего его в 1824 году французского инженера. Данное явление впоследствии оказало колоссальное влияние на развитие учения о тепловых процессах.
Рисунок 3 . 11 . 5 . Цикл Карно.
Находящийся в цилиндре, под поршнем, газ совершает цикл Карно. На участке изотермы ( 1 – 2 ) он приводится в тепловой контакт с нагревателем, обладающим некоторой температурой T 1 . Газ изотермически расширяется, при этом к нему подводится эквивалентное совершенной работе A 12 количество теплоты Q 1 = A 12 . После этого на участке адиабаты ( 2 – 3 ) газ помещается в адиабатическую оболочку и продолжает процесс расширения при отсутствующем теплообмене. На данной части цикла газ совершает работу A 23 > 0 . Его температура при адиабатическом расширении снижается до величины T 2 . На идущем следующим участке изотермы ( 3 – 4 ) газ приводится в тепловой контакт с холодильником в условиях температуры T 2 T 1 . Производится процесс изотермического сжатия. Газом совершается некоторая работа A 34 0 и отдается тепло Q 2 0 , эквивалентное произведенной им работе A 34 . Его внутренняя энергия не претерпевает изменений. На последнем оставшемся участке адиабатического сжатия газ снова помещают в адиабатическую оболочку. При сжатии его температура вырастает до величины T 1 , также совершается работа A 41 0 . совершаемая газом за цикл полная работа A эквивалентна сумме работ на отдельных участках:
A = A 12 + A 23 + A 34 + A 41 .
На диаграмме ( p , V ) данная работа равняется площади цикла.
Процессы на любом из участков цикла Карно квазистатичны. Например, оба участка 1 – 2 и 3 – 4 , относящихся к изотермическим, производятся при пренебрежительно малой разности температур рабочего тела, то есть газа, и теплового резервуара, будь то нагреватель или холодильник.
Исходя из первого закона термодинамики, можно заявить, что работа газа в условиях адиабатического расширения или сжатия эквивалентна падению значения Δ U его внутренней энергии. Для 1 моля газа верно следующее выражение:
A = — ∆ U = — C V ( T 2 — T 1 ) ,
в котором T 1 и T 2 представляют собой начальную и конечную температуры рабочего тела.
Из этого следует, что работы, совершаемые газом на двух адиабатических участках цикла Карно, противоположны по знакам и одинаковы по модулю:
Коэффициент полезного действия η цикла Карно может рассчитываться с помощью следующих соотношений:
η = A Q 1 = A 12 + A 34 Q 12 = Q 1 — Q 2 Q 1 = 1 — Q 2 Q 1 .
С. Карно выразил коэффициент полезного действия цикла через величины температур холодильника T 2 и нагревателя T 1 :
η = T 1 — T 2 T 1 = 1 — T 2 T 1 .
Цикл Карно примечателен тем, что ни на одном из его участков тела, обладающие различными температурами, не соприкасаются. Любое состояние рабочего тела в цикле является квазиравновесным, что означает его бесконечную близость к состоянию теплового равновесия с окружающими объектами, то есть тепловыми резервуарами или же термостатами. В цикле Карно исключен теплообмен в условиях конечной разности температур рабочего тела и окружающей среды (термостатов), если тепло имеет возможность переходить без совершения работы. По этой причине любые другие возможные круговые процессы проигрывают ему в эффективности при заданных температурах нагревателя и холодильника:
η К а р н о = η m a x
Рисунок 3 . 11 . 6 . Модель цикла Карно.
Каждый участок цикла Карно и цикл в целом могут проходиться в обоих направлениях.
Обход цикла по часовой стрелке соответствует тепловому двигателю, в котором полученное рабочим телом тепло частично преобразуется в полезную работу. Обход против часовой стрелки соответствует холодильной машине, где некое количество теплоты отходит от холодного резервуара и передается горячему резервуару за счет совершения внешней работы. Именно поэтому идеальное устройство, работающее по циклу Карно, носит название обратимой тепловой машины.
В реально существующих холодильных машинах применяются разные циклические процессы. Любой холодильный цикл на диаграмме ( p , V ) обходятся против часовой стрелки. На рисунке 3 . 11 . 7 проиллюстрирована энергетическая схема холодильной машины.
Рисунок 3 . 11 . 7 . Энергетическая схема холодильной машины. Q 1 0 , A > 0 , Q 2 > 0 , T 1 > T 2 .
Работающее по холодильному циклу устройство может обладать двояким предназначением.
Если полезным эффектом является отбор некоторого количества тепла Q 2 от охлаждаемых тел, к примеру, от продуктов в камере холодильника, то такое устройство является обычным холодильником.
Эффективность работы холодильника может быть охарактеризована следующим отношением:
Таким образом, эффективность работы холодильника представляет собой количество тепла, отбираемого от охлаждаемых тел на 1 д ж о у л ь затраченной работы. В условиях подобного определения β х может быть, как больше, так и меньше единицы. Для обращенного цикла Карно справедливо выражение:
β x = T 2 T 1 — T 2 .
В случае, когда полезным эффектом является передача некоего количества тепла
| Q 1 | нагреваемым телам, чьим примером может выступать воздух в помещении, то такое устройство называется тепловым насосом.
Эффективность β Т теплового насоса может быть определена с помощью отношения:
То есть она может определяться количеством теплоты, передаваемым более теплым телам на 1 д ж о у л ь затраченной работы. Из первого закона термодинамики следует:
Следовательно, β Т всегда больше единицы. Для обращенного цикла Карно справедливо следующее выражение: