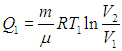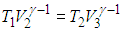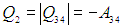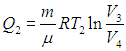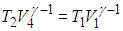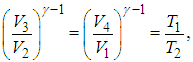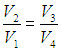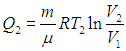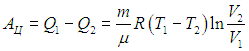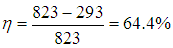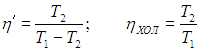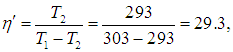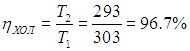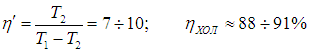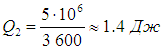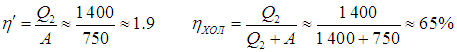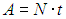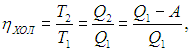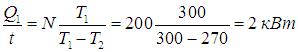- Работа газа тепловой машины карно формула
- 5.2. Цикл Карно
- wiki.eduVdom.com
- Инструменты пользователя
- Инструменты сайта
- Боковая панель
- Содержание
- Тепловые машины. Цикл Карно
- Примеры тепловых двигателей
- КПД тепловой машины
- Цикл Карно
- Схема цикла Карно
- Иллюстрации цикла Карно
- Цикл Карно
- Максимальный КПД тепловой машины
Работа газа тепловой машины карно формула
Найдем полезную работу цикла Карно.
Процесс А–В. Положительная работа, совершенная газом при изотермическом расширении одного моля газа от V0 до V1.
Тепло, полученное от нагревателя Q1, идет на изотермическое расширение газа, совершая при этом работу А1:
Уравнение адиабаты: 
Давление при этом изменится до Р2. Полученная работа на этой стадии:
Уравнение адиабаты: 
Работа сжатия на последнем этапе:
Работа равна площади ограниченной кривой АВСDА.
5.2. Цикл Карно
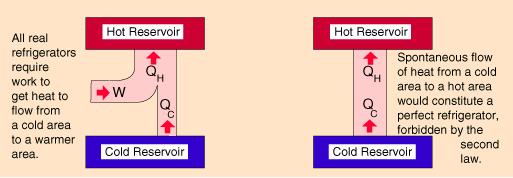
Для работы любой тепловой машины по замкнутому циклу необходима внешняя среда, которую условно можно представить себе как два тела — нагреватель, находящийся при температуре Тmах, и холодильник, находящийся при температуре Tmin (Tmin (2.13) 
Адиабата 2—3. Здесь система отсоединяется от нагревателя и не обменивается теплом с внешней средой: Q23 = 0. Газ продолжает расширяться, но уже адиабатно. Работа совершается за счет внутренней энергии газа, и его температура падает до значения Т2. На этом участке цикла нам нужна информация, доставляемая уравнением адиабаты:
Изотерма 3—4. Система подключается к холодильнику, и газ начинает сжиматься. Внутренняя энергия остается неизменной, над газом совершается работа (А34 < 0), а выделяющееся
передается холодильнику. Имеем аналогично (5.6)
Адиабата 4—1. Система отключена от внешней среды и продолжает сжиматься изотермически, что приводит к повышению ее температуры до Т1. В конечном итоге система возвращается в первоначальное состояние. Поскольку точки 4 и 1 лежат на адиабате, получаем связь объемов и температур, аналогичную (5.7):
Из уравнений (5.7) и (5.9) находим отношения объемов
откуда следует, что
Поэтому отдаваемую холодильнику теплоту Q2 (см. уравнение (5.8)) можно записать как
Используя выражение (5.6) для теплоты, полученной системой, находим совершенную в ходе цикла работу
Из проведенного анализа следует также, что максимальная температура в цикле равна Тmах = Т1, а минимальная — Тmin = Т2. Если разделить (5.12) на (5.6), то немедленно получим выражение (5.5) для КПД цикла Карно, из которого выпадают все параметры, кроме температур холодильника и нагревателя.
Пример 1. Котел тепловой станции работает при температуре около t1 = 550 °С. Отработанное тепло отводится к реке при температуре около t2 = 20 °С. Найдем максимально возможный КПД этой станции (рис. 5.4).
Рис. 5.4. Схема работы тепловой машины Карно
Поскольку в формуле для КПД цикла Карно используются абсолютные температуры, надо перейти от шкалы Цельсия к шкале Кельвина: Т1 = 550 + 273 = 823 К, Т2 = 20 + 273 = 293 К. Теперь находим КПД тепловой станции:
Конечно, реальный КПД станции заметно ниже.
Если цикл Карно осуществить в обратном направлении, то есть против часовой стрелки на рис. 5.2, то для определения эффективности холодильной установки надо использовать формулы (5.3), (5.4) и выражения (5.6), (5.11). Получаем тогда
Печально, но чем ниже температура внешней среды Т1, тем меньше мы нуждаемся в холодильнике, и тем эффективнее он работает.
Рис. 5.5. Схема работы холодильной установки
Приведем численный пример. Если кондиционер поддерживает в комнате температуру t2 = 20 °С, а температура наружного воздуха равна t1 = 30 °С, то для холодильного коэффициента имеем
а для КПД холодильника
Конечно, на самом деле температура тепловыделяющего элемента больше наружной температуры на 20–30 градусов, так что разность температур может достигать 30–40 градусов, что приводит к значениям
Напомним, что речь идет об идеальных установках, работающих по циклу Карно. Реальный типичный кондиционер потребляет мощность 750 Вт, перекачивая за час около 5 МДж тепловой энергии. Это значит, что за секунду кондиционер совершает работу А = 750 Дж и отнимает у воздуха в комнате теплоту
Мы видим, что реальный кондиционер гораздо менее эффективен, нежели идеальный холодильник Карно.
Пример 2. Пусть в домашнем холодильнике поддерживается температура t2 = –3 °С (Т2 = 270 К), а температура в кухне равна t1 = 27 °С (T1 = 300 К). Пусть далее мотор холодильника потребляет мощность N = 200 Вт. Предполагая, что холодильник работает по циклу Карно и что тепловыделяющий элемент имеет температуру окружающего воздуха, определим мощность потока тепловой энергии, перекачиваемой из камеры холодильника в кухню.
За время t мотор совершит работу
КПД холодильника равен
откуда находим количество теплоты, поступающее в кухню в единицу времени:
Обратите внимание, что холодильник работает как весьма эффективный обогреватель помещения. Надо только оплачивать потребляемую мотором мощность 200 Вт, а в кухню поступит в 10 раз большая энергия, 90 % которой перекачивается из камеры холодильника (90 % — КПД холодильника в этом примере). Любопытно, что если бы вместо холодильника был включен обогреватель той же мощности, то он нагревал бы помещение в 10 раз слабее.
Наши численные оценки можно рассматривать как пример теплового загрязнения окружающей среды, свойственного технической цивилизации.
wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Физика:
Контакты
Содержание
Тепловые машины. Цикл Карно
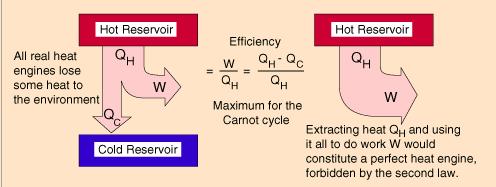
В современной технике механическую энергию получают главным образом за счёт внутренней энергии топлива. Устройства, в которых происходит преобразование внутренней энергии в механическую, называют тепловыми двигателями.
Примеры тепловых двигателей
КПД тепловой машины
Работа, совершаемая тепловой машиной, не может быть больше: $A = Q_ <1>— |Q_<2>|$, т.к. рабочее тело, получая некоторое количество теплоты ($Q_<1>$) от нагревателя , часть этого количества теплоты (по модулю равную $|Q_<2>|$) отдаёт холодильнику . Отношение этой работы к количеству теплоты, полученному расширяющимся газом от нагревателя, называется коэффициентом полезного действия $\eta$ тепловой машины.
Коэффициент полезного действия любой тепловой машины считается по формуле: $$\eta = \frac
Для увеличения КПД, при расширении или сжатии газа должны быть использованы процессы, позволяющие исключить уменьшение энергии горячего тела, которое происходило бы без совершения работы. Такие процессы существуют — это изотермический и адиабатный процесс.
Цикл Карно
Сади Карно искал пути решения актуальной для его времени задачи — установить причину несовершенства тепловых машин, найти пути наиболее эффективного их использования. Именно он, впервые предложил наиболее совершенный технический процесс, состоящий из изотерм и адиабат.
Схема цикла Карно
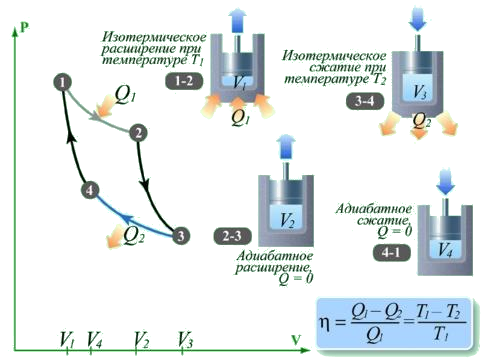
Прямой цикл Карно. Исходным состоянием рабочего тела двигателя является состояние точки 4 . На участке 4—1 цикла рабочее тело сжимается адиабатически, т. е. без потерь теплоты. В точке 1 к нему начинают изотермически подводить теплоту $Q_<1>$ от высокотемпературного источника, в результате чего рабочее тело расширяется по линии 1—2 . На участке 2—3 расширение рабочего тела продолжается уже без подвода теплоты, т. е. адиабатически. На участке 3—4 от рабочего тела с помощью источника низкой температуры отбирается теплота $Q_<2>$. В двигателях, работающих по разомкнутому циклу, когда теплоноситель в каждом цикле работы обновляется, процесс охлаждения заменяется процессом обновления теплоносителя.
| Линия | Состояние | Описание | |
|---|---|---|---|
| 1-2 | Изотерма $T=T_<1>$ $dQ_<1>$ (нагревание) $V\Uparrow$ | От нагревателя поступает теплота $dQ_<1>$ (или $Q_ | В начале процесса рабочее тело ( газ ) имеет температуру температуру нагревателя ($T_ При этом объём рабочего тела увеличивается, оно совершает механическую работу, а его энтропия возрастает. |
| 2-3 | Адиабата | ||
$dQ=0$
$V\Uparrow$
При этом температура тела уменьшается до температуры холодильника ($T_
$T=T_<2>$
$dQ_<2>$
(охлаждение)
$V\Downarrow$
Над телом совершается работа, его энтропия уменьшается.
$dQ=0$
$V\Downarrow$
При этом его температура увеличивается до температуры нагревателя ($T_
Иллюстрации цикла Карно
Цикл Карно
Максимальный КПД тепловой машины
Коэффициент полезного действия идеального цикла, как показал С.Карно, может быть выражен через температуру нагревателя ($T_<1>$) и холодильника ($T_<2>$). В реальных двигателях не удаётся осуществить цикл, состоящий из идеальных изотермических и адиабатных процессов. Поэтому КПД их цикла всегда меньше, чем КПД цикла Карно (при прочих равных условиях). $$\eta_
При этом чем меньше разность температур между холодильной камерой и окружающей средой, тем меньше нужно затратить энергии для передачи теплоты от холодного тела к горячему и тем выше холодильный коэффициент.
Анализ обратного цикла Карно показывает, что передача теплоты от тела менее нагретого телу более нагретому возможна, но этот процесс требует соответствующей энергетической компенсации в системе, в виде затраченной работы или теплоты более высокого потенциала, способного совершить работу при переходе на более низкий потенциал.
Энтропия — часть внутренней энергии замкнутой системы или энергетической совокупности Вселенной, которая не может быть использована, в частности не может перейти или быть преобразована в механическую работу. Существует мнение, что мы можем смотреть на энтропию и как на меру беспорядка в системе.