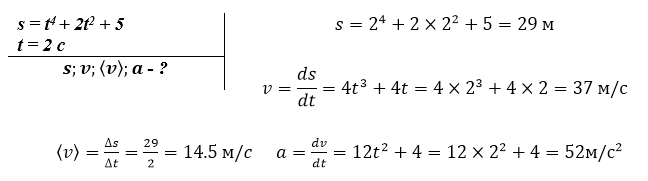Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях – решение задачи

Основные законы и формулы, применяемые при решении задач

Вращательное движение вокруг неподвижной оси

Рассмотри твердое тело, вращающееся вокруг неподвижной оси z . Сделаем рисунок. Ось вращения направим перпендикулярно плоскости рисунка, на нас. Пусть φ – угол поворота тела вокруг оси, отсчитываемый от некоторого начального положения. За положительное направление выберем направление против часовой стрелки. Угловая скорость ω равна производной угла поворота по времени t :
.
При , тело вращается против часовой стрелки; при – по часовой. Вектор угловой скорости направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

Угловое ускорение ε равно производной угловой скорости по времени:
.
Вектор углового ускорения также направлен перпендикулярно плоскости рисунка. При он направлен на нас; при – от нас.

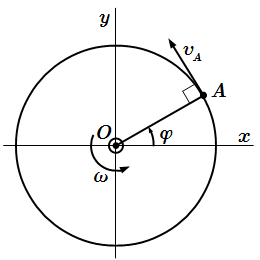
Скорость точки при вращательном движении тела вокруг неподвижной оси

Рассмотрим точку A , принадлежащую твердому телу. Опустим из нее перпендикуляр OA на ось вращения. Пусть – расстояние от точки до оси. Траекторией движения точки A является окружность (или дуга) с центром в точке O радиуса .

Абсолютное значение скорости точки A определяется по формуле:
.
Вектор скорости направлен по касательной к траектории (окружности), перпендикулярно отрезку OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор угловой скорости .

Касательное (или тангенциальное) ускорение точки A определяется аналогично скорости:
.
Оно направлено по касательной к окружности, перпендикулярно OA . При этом вектор должен производить закручивание в ту же сторону, что и вектор углового ускорения .

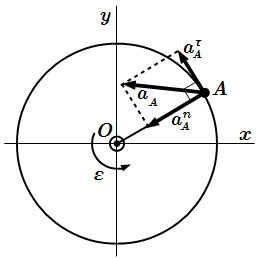
Ускорение точки при вращательном движении тела вокруг неподвижной оси

Нормальное ускорение всегда направлено к центру окружности и имеет абсолютную величину
.

Полное ускорение точки A , или просто ускорение, равно векторной сумме касательного и нормального ускорений:
.
Поскольку векторы и перпендикулярны, то абсолютная величина ускорения точки A определяется по формуле:
.

Поступательное прямолинейное движение

Теперь рассмотрим прямолинейное поступательное движение тела. Направим ось x вдоль его линии движения. Пусть s есть перемещение тела вдоль этой оси относительно некоторого начального положения. Тогда скорость движения всех точек тела равна производной перемещения по времени:
.
При , вектор скорости направлен вдоль оси x . При – противоположно этой оси.

Ускорение точек тела равно производной скорости по времени, или второй производной перемещения по времени:
.
При , вектор ускорения направлен вдоль оси x . При – противоположно.

Соприкосновение тел без проскальзывания

Рассмотрим два тела, находящиеся в зацеплении без проскальзывания. Пусть точка A принадлежит первому телу, а точка B – второму. И пусть, в рассматриваемый момент времени, положения этих точек совпадают. Тогда, если между телами нет проскальзывания, то скорости этих точек равны:
.
Если каждое из тел вращается вокруг неподвижной оси, то равны соответствующие касательные ускорения:
.
Если одно из тел движется поступательно (пусть это второе тело), то ускорение его точек равно касательному ускорению точки соприкосновения первого тела:
.

Пример решения задачи

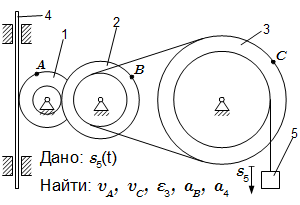
Механизм состоит из ступенчатых колес 1, 2, 3, находящихся в зацеплении и связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес. Радиусы ступеней колес равны соответственно: у колеса 1 – r₁ = 2 см, R₁ = 4 см, у колеса 2 – r₂ = 6 см, R₂ = 8 см, у колеса 3 – r₃ = 12 см, R₃ = 16 см. На ободьях колес расположены точки A, B и C. Задан закон движения груза: s₅ = t 3 – 6t (см). Положительное направление для s₅ – вниз.

Определить в момент времени t = 2 скорости точек A, C; угловое ускорение колеса 3; ускорение точки B и ускорение рейки 4.

Указания. Эта задача – на исследование вращательного движения твердого тела вокруг неподвижной оси. При решении задачи учесть, что проскальзывание в ременной передаче и в точках сцепления колес отсутствует. То есть скорости точек колес, находящихся в зацеплении равны, а скорости точек ремня равны скорости точек, лежащих на ободе колес, связанных ременной передачей.

Дано:
t = 2 с; r₁ = 2 см, R₁ = 4 см; r₂ = 6 см, R₂ = 8 см; r₃ = 12 см, R₃ = 16 см; s₅ = t 3 – 6t (см).

Определение скорости и ускорения груза 5

Груз 5 совершает поступательное движение. Поэтому скорости (и ускорения) всех его точек равны. В условии задачи задано смещение s груза относительно некоторого начального положения. Дифференцируя по времени t , находим зависимость скорости точек груза от времени:
.
Дифференцируя скорость груза по времени, находим зависимость ускорения груза от времени:
.

Находим скорость и ускорение груза в заданный момент времени :
см/с;
см/с 2 .

Определение угловых скоростей и ускорений колес

Груз 5 связан нитью с внутренним ободом колеса 3. Поэтому скорости точек внутреннего обода колеса 3 равны скорости груза:
.
Отсюда находим угловую скорость колеса 3 для произвольного момента времени:
.
Здесь подразумевается, что и являются функциями от времени t . Дифференцируя по t , находим угловое ускорение колеса 3:
.
Находим значения угловой скорости и углового ускорения в момент времени с. Для этого подставляем найденные значения и при с:
с –1 ;
с –2 .

Рассмотрим колесо 2. Его внутренний обод связан нитью с внешним ободом колеса 3. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 2 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Рассмотрим колесо 1. Его внутренний обод находится в зацеплении с внешним ободом колеса 2. Поэтому скорости точек на этих ободьях равны:
. Отсюда
.
Дифференцируя по времени, находим угловое ускорение колеса 1 в произвольный момент времени:
.
Подставляем значения для с:
с –1 ;
с –2 .

Итак, мы нашли:
ω ₁ = 5.3333 с –1 , ω ₂ = 1.3333 с –1 , ω ₃ = 0.5 с –1 , ε ₁ = 10.6667 с –2 , ε ₂ = 2.6667 с –2 , ε ₃ = 1 с –2 .

Определение скоростей точек A и C

Точка A лежит на окружности радиуса R₁ с центром в точке O₁, расположенной на оси вращения. Поэтому скорость этой точки направлена по касательной к окружности и по абсолютной величине равна
см/с.

Точка C лежит на окружности радиуса R₃ с центром O₃ на оси вращения. Скорость этой точки:
см/с.

Определение ускорения точки B

Точка B лежит на окружности радиуса R₂ с центром O₂, расположенном на оси вращения. Касательное (или тангенциальное) ускорение этой точки направлено по касательной к окружности в сторону, на которую указывает угловое ускорение (по часовой стрелке). По абсолютной величине оно равно
см/с 2 .

Нормальное ускорение всегда направлено к центру окружности. По абсолютной величине оно равно
см/с 2 .

Полное ускорение равно векторной сумме касательного и нормального ускорений:
.
Поскольку касательное ускорение перпендикулярно нормальному, то для абсолютной величины полного ускорения имеем:
см/с 2 .

Определение ускорения рейки 4

Рейка 4 движется поступательно по направляющим. Она находится в зацеплении с внешним ободом колеса 1. Поэтому ее скорость равна скорости точек внешнего обода колеса 1:
.
Дифференцирую по времени, получаем ускорение рейки в произвольный момент времени:
.
Подставляем численные значения для момента времени t = 2 с :
см/с 2 .

см/с; см/с; с –2 ; см/с 2 ; см/с 2 .

Автор: Олег Одинцов . Опубликовано: 25-10-2019

При поступательно вращательном движении колес автомобиля образуется

Существует пять видов движения твердого тела:

1. поступательное движение;
2. вращение вокруг неподвижной оси;
3. плоское движение;
4. вращение вокруг неподвижной точки;
5. свободное движение.

Первые два называются простейшими движениями твердого тела. Остальные виды движений можно представить как комбинацию основных движений.

Поступательным называется такое движение твердого тела, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной своему начальному направлению.

Любое прямолинейное движение является поступательным. Однако поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями.

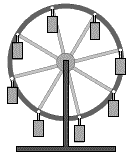
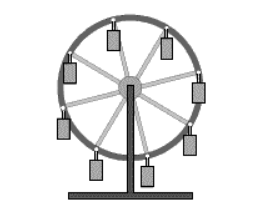
Рис.1 Поступательное криволинейное движение кабин колеса обзора

Готовые работы на аналогичную тему

Свойства поступательного движения определяются следующей теоремой: при поступательном движении все точки тела описывают одинаковые (при наложении совпадающие) траектории и имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения.

Из теоремы следует, что поступательное движение твердого тела определяется движением какой-нибудь одной из его точки. Следовательно, изучение поступательного движения тела сводится к задаче кинематике точки.

При поступательном движении общую для всех точек тела скорость $\overrightarrow $ называют скоростью поступательного движения тела, а ускорение $\overrightarrow $ — ускорением поступательного движения тела. Векторы $\overrightarrow $ и $\overrightarrow $ можно изображать приложенными в любой точке тела.

Заметим, что понятие о скорости и ускорении тела имеют смысл только при поступательном движении. Во всех остальных случаях точки тела, движутся с разными скоростями и ускорениями, и термины «скорость тела» или «ускорение тела» для этих движений теряют смысл.

Вращательным движением абсолютно твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела движутся в плоскостях, перпендикулярных к неподвижной прямой, называемой осью вращения, и описывают окружности, центры которых лежат на этой оси.

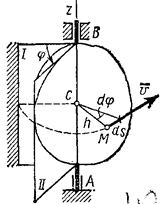
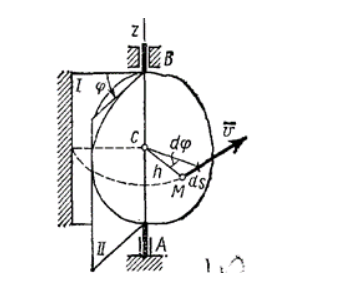
Для определения положения вращающегося тела проведем через ось вращения, вдоль которой направим ось Az, полуплоскость — неподвижную и полуплоскость, врезанную в само тело и вращающуюся вместе с ним (рис. 2).

Рисунок 2. Угол поворота тела

Тогда положение тела в любой момент времени однозначно определится взятым с соответствующим знаком углом $\varphi $ между этими полуплоскостями, который назовем углом поворота тела. Будем считать угол $\varphi $ положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного конца оси Az), и отрицательным, если по ходу часовой стрелки. Измерять угол $\varphi $ будем всегда в радианах. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла $\varphi $ от времени t, т.е. $<\mathbf \varphi >$=f(t). Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси.

При вращательном движении абсолютно твердого тела вокруг неподвижной оси углы поворота радиуса-вектора различных точек тела одинаковы.

Основными кинематическими характеристиками вращательного движения твердого тела являются его угловая скорость $\omega $ и угловое ускорение $\varepsilon $.

Уравнения, описывающие вращательное движение, можно получить из уравнений поступательного движения, произведя в последних следующие замены: перемещение s — угловое перемещение (угол поворота) $\varphi $, скорость u — угловая скорость $\omega $, ускорение a — угловое ускорение $\varepsilon $.

Материальная точка движется по прямой. Уравнение ее движения $s = t^4 + 2t^2 + 5$. Определить мгновенную скорость и ускорение точки в конце второй секунды от начала движения, среднюю скорость и путь, пройденный за это время.

Тело вращается вокруг неподвижной оси. Уравнение его движения $<\mathbf \varphi >$ = $t^4 + 2t^2 + 5$. Определить мгновенную угловую скорость и угловое ускорение тела в конце второй секунды от начала движения, среднюю угловую скорость и угол поворота за это время.

Поступательное и вращательное движение

Движение твердого тела разделяют на виды:

• поступательное;
• вращательное по неподвижной оси;
• плоское;
• вращательное вокруг неподвижной точки;
• свободное.

Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.

Поступательное криволинейное движение. Угол поворота тела

Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.

Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.

Рисунок 1 . Поступательное криволинейное движение кабин колеса обзора

Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.

Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.

Если имеется поступательное движение, то общая скорость для всех точек тела υ → называется скоростью поступательного движения, а ускорение a → — ускорением поступательного движения. Изображение векторов υ → и a → принято указывать приложенными в любой точке тела.

Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.

Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.

Чтобы определить положение вращающегося тела, необходимо начертить ось вращения, вдоль которой направляется ось A z , полуплоскость – неподвижную, проходящую через тело и движущуюся с ним, как показано на рисунке 2 .

Рисунок 2 . Угол поворота тела

Положение тела в любой момент времени будет характеризоваться соответствующим знаком перед углом φ между полуплоскостями, который получил название угол поворота тела. При его откладывании, начиная от неподвижной плоскости (направление против хода часовой стрелки), угол принимает положительное значение, против плоскости – отрицательное. Измерение угла производится в радианах. Для определения положения тела в любой момент времени следует учитывать зависимость угла φ от t , то есть φ = f ( t ) . Уравнение является законом вращательного движения твердого тела вокруг неподвижной оси.

При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.

Вращательное движение твердого тела характеризуется угловой скоростью ω и угловым ускорением ε .

Уравнения вращательного движения получают из уравнений поступательного, используя замены перемещения S на угловое перемещение φ , скорость υ на угловую скорость ω , а ускорение a на угловое ε .

Вращательное и поступательное движение. Формулы

Поступательное	Вращательное
Равномерное
s = υ · t	φ = ω · t
υ = c o n s t	ω = c o n s t
a = 0	ε = 0
Равнопеременное
s = υ 0 t ± a t 2 2	φ = ω 0 t ± ε · t 2 2
υ = υ 0 ± a · t	ω = ω 0 ± ε · t
a = c o n s t	ε = c o n s t
Неравномерное
s = f ( t )	φ = f ( t )
υ = d s d t	ω = d φ d t
a = d υ d t = d 2 s d t 2	ε = d ω d t = d 2 φ d t 2

Задачи на вращательное движение

Дана материальная точка, которая движется прямолинейно соответственно уравнению s = t 4 + 2 t 2 + 5 . Вычислить мгновенную скорость и ускорение точки в конце второй секунды после начала движения, среднюю скорость и пройденный за этот промежуток времени путь.

Дано: s = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: s ; υ ; » open=» υ ; α .

Решение

s = 2 4 + 2 · 2 2 + 5 = 29 м .

υ = d s d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 м / с .

» open=» υ = ∆ s ∆ t = 29 2 = 14 , 5 м / с .

a = d υ d t = 12 t 2 + 4 = 12 · 2 2 + 4 = 52 м / с 2 .

Ответ: s = 29 м ; υ = 37 м / с ; » open=» υ = 14 , 5 м / с ; α = 52 м / с 2

Задано тело, вращающееся вокруг неподвижной оси по уравнению φ = t 4 + 2 t 2 + 5 . Произвести вычисление мгновенной угловой скорости, углового ускорения тела в конце 2 секунды после начала движения, средней угловой скорости и угла поворота за данный промежуток времени.

Дано: φ = t 4 + 2 t 2 + 5 , t = 2 с .

Найти: φ ; ω ; » open=» ω ; ε .

Решение

φ = 2 4 + 2 · 2 2 + 5 = 29 р а д .

ω = d φ d t = 4 t 3 + 4 t = 4 · 2 3 + 4 · 2 = 37 р а д / с .

» open=» ω = ∆ φ ∆ t = 29 2 = 14 , 5 р а д / с .

ε = d ω d t = 12 2 + 4 = 12 · 2 2 + 4 = 52 р а д / с 2 .

Ответ: φ = 29 р а д ; ω = 37 р а д / с ; » open=» ω = 14 , 5 р а д / с ; ε = 52 р а д / с 2 .