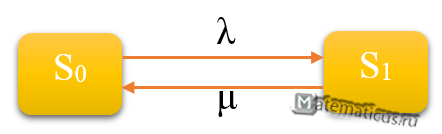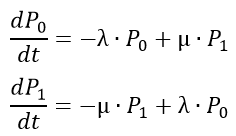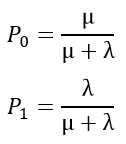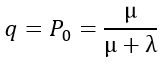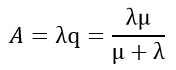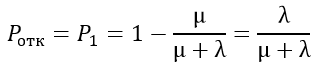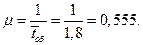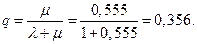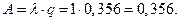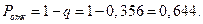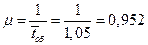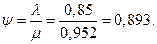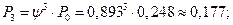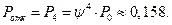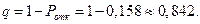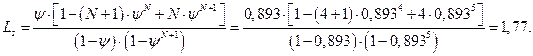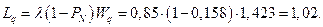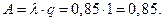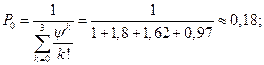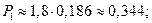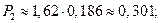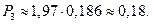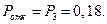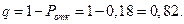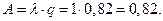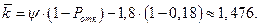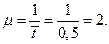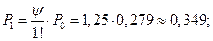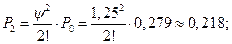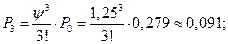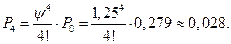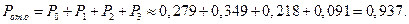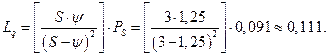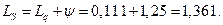Одноканальная СМО с отказами

Одноканальная СМО (система массового обслуживания) с отказами, означает, что СМО состоит из одного канала обслуживания и если канал занят, то транзакт (заявка) покидает систему обслуживания.

Граф состояний одноканальной СМО с отказами

S₀ – канал свободен;

S₁ – канал занят.

Дифференциальное уравнение Колмогорова

P ₀ — вероятность обслуживания заявки;

P ₁ — вероятность отказа;

Отсюда находим значения вероятностей нахождения СМО с отказами в состояниях S₀ и S₁

Относительная пропускная способность q определяется по формуле

Абсолютная пропускная способность A находится по формуле

Вероятность отказа равна P_отк:

Основателем теории массового обслуживания является А.К. Эрланг 1900-1930 гг. Данная теория начала развиваться, прежде всего, в телефонии.

ОДНОКАНАЛЬНАЯ СМО С ОТКАЗАМИ

Рассмотрим простейшую из всех задач теории массового обслу­живания – задачу о функционировании одноканальной СМО с отка­зами.

Пусть система массового обслуживания состоит только из одного канала (n=1) и на нее поступает пуассоновский поток заявок с ин­тенсивностью λ, зависящей, в общем случае, от времени:

Заявка, заставшая канал занятым, получает отказ и покидает си­стему.

Обслуживание заявки продолжается в течение случайного времени T_об, распределенного по показательному закону с параметром μ:

f(t) = μ e -μ t (t>0). (3.2)

Из этого следует, что «поток об­служиваний» — простейший, с интенсивностью μ. Чтобы представить
себе реально этот поток, вообразим один непрерывно занятый канал – он будет выдавать обслуженные заявки потоком с интенсивностью μ.

1) абсолютную пропускную способность СМО (А);

2) относительную пропускную способность СМО (q).

Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в одном из двух состояний:

Граф состояний системы показан на рис. 1.

Из состояния S₀ в S₁ систему, очевидно, переводит поток заявок с интенсивностью λ; из S₁ и S₀ – «поток обслуживании» с интенсив­ностью μ.

Обозначим вероятности состояний p₀(t) и р₁(t). Очевидно, для лю­бого момента t:

Составим дифференциальные уравнения Колмогорова для вероят­ностей состояний согласно правилу, данному в предыдущем разделе. Имеем:

(3.4)

Из двух уравнений (3.4) одно является лишним, так как p₀ и р₁ свя­заны соотношением (3.3). Учитывая это, отбросим второе уравнение, а в первое подставим вместо р₁ его выражение (1– p₀):

(3.5)

Это уравнение естественно решать при начальных условиях:

Линейное дифференциальное уравнение (3.5) с одной неизвестной функцией p₀ легко может быть решено не только для простейшего по­тока заявок (λ = const), но и для случая, когда интенсивность этого потока со временем меняется (λ=λ(t)). He останавливаясь на последнем случае, приведем реше­ние уравнения (3.5) только для случая λ= const:

(3.6)

Зависимость величины p₀ от времени имеет вид изображенный на рис. 2. В начальный момент (при t=0)

канал заведомо свободен ( p₀(0)=1 ).

С увеличением t вероятность p₀ уменьшается и в пределе (при t→∞) равна 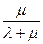. Величина p₀(t), дополняющая p₀(t) до единицы, изменяется как показано на том же рис. 2.

Нетрудно убедиться, что для одноканальной СМО с отказами ее вероятность p₀ есть не что иное, как относительная пропускная способ­ность q.

Действительно, p₀ есть вероятность того, что в момент t канал сво­боден, иначе вероятность того, что заявка, пришедшая в момент t, будет обслужена. А значит, для данного момента времени t среднее от­ношение числа обслуженных заявок к числу поступивших также рав­но p₀: q= p₀.

В пределе, при t→∞, когда процесс обслуживания уже устано­вится, предельное значение относительной пропускной способности будет равно:

q = 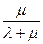(3.7)

Зная относительную пропускную способность q, легко найти аб­солютную A. Они связаны очевидным соотношением:

В пределе, при t→∞, абсолютная пропускная способность тоже установится и будет равна

A = 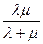. (3.9)

Зная относительную пропускную способность системы q (вероят­ность того, что пришедшая в момент t заявка будет обслужена), легко найти вероятность отказа:

Вероятность отказа Р_отк есть не что иное, как средняя до­ля необслуженных заявок среди поданных. В пределе, при t→∞,

Р_отк = 1 – 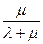= (3.11)

Пример. Одноканальная СМО с отказами представляет собой одну теле­фонную линию. Заявка – вызов, пришедший в момент, когда линия занята, получает отказ. Интенсивность потока вызовов λ = 0,8 (вызовов в минуту). Средняя продолжительность разговора t_об = 1,5 мин. Все потоки событий – про­стейшие. Определить предельные (при t→∞) значения:

1) относительной пропускной способности q;

2) абсолютной пропускной способности А;

3) вероятности отказа Р_отк.

Сравнить фактическую пропускную способность СМО с номинальной, ко­торая была бы, если бы каждый разговор длился в точности 1,5 мин, и разгово­ры следовали бы один за другим без перерыва.

Решение. Определяем параметр μ потока обслуживаний:

По формуле (3.6) получаем относительную пропускную способность СМО:

q = = 0,455.

Таким образом, в установившемся режиме система будет обслуживать около 45% поступающих вызовов.

По формуле (3.9) находим абсолютную пропускную способность:

т. е. линия способна осуществить в среднем 0,364 разговора в минуту. Вероятность отказа:

значит около 55% поступивших вызовов будет получать отказ.

Номинальная пропускная способность канала:

что почти вдвое больше, чем фактическая пропускная способность, получаемая с учетом случайного характера потока заявок и случайности времени обслужи­вания.

Примеры задач для одноканальных СМО

Одноканальная СМО с отказами в обслуживании

1. Пункт по ремонту радиотехники работает в режиме отказа с одним мастером. Интенсивность потока заявок λ, производительность мастера μ. Определить предельные значения относительной пропускной способности Q, абсолютной пропускной способности А и вероятность отказа Ротк телефонной линии. Определить также среднее время обслуживания одного вызова, среднее время простоя канала и вероятность того, что канал свободен или занят.
Скачать решение

2. Статистическими исследованиями в результате наблюдения установлено, что интенсивность потока телефонных звонков коммерческому директору λ = 1.2 вызова в минуту, средняя продолжительность разговора (обслуживания заявки) t_обсл = 2.5 мин и все потоки событий (вызовов и обслуживания) имеют характер простейших пуассоновских потоков.
Определим предельную (относительную и абсолютную) пропускную способность СМО, вероятность отказа, а также полное число обслуженных и необслуженных (получивших отказ) заявок в течение 1 ч работы СМО. Сравнить фактическую пропускную способность СМО с номинальной, т.е. с пропускной, способностью, которой обладала бы система в том случае, если бы каждая заявка обслуживалась ровно 2,5 мин и все заявки следовали бы одна за другой без перерыва.

Рекомендации к решению задачи: здесь λ = 1.2 ед. в мин.; t = 2.5 мин. или μ = 0.4 заявки в мин.

3. Рабочий обслуживает m станков. Поток требований на обслуживание пуассоновский с параметром λ станков в час. Время обслуживания одного станка подчинено экспоненциальному закону. Среднее время обслуживания одного станка равна μ минут. Определить: 1) среднее число станков, ожидающих обслуживания, 2) коэффициент простоя станка, 3) коэффициент простоя рабочего.
n=1, m=3, λ=2, μ=8.

Одноканальная СМО с ограниченной длиной очереди

1. В магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 2 покупателя в минуту. В этом магазине установлен один кассовый аппарат, позволяющий добиться такой производительности труда, при которой интенсивность потока обслуживания составляет величину μ = покупателя в минуту. Определим характеристики СМО при условии, что очередь ограничена контролером при входе в зал самообслуживания: m = 5 покупателям.

2. На автомойку в среднем за час приезжают три автомобиля, если в очереди уже находятся два автомобиля, то вновь подъезжающие автомобили не желают терять время в ожидании обслуживания и покидают мойку, поскольку среднее время мойки одного автомобиля составляет 20 мин, а мест для мойки всего одно. Необходимо провести анализ работы системы обслуживания с 9-00 до 21-00 ч, если средняя стоимость мойки одного автомобиля составляет 70 руб.

Рекомендации к решению задачи: здесь m = 2; λ = 3 ед. в час.; t_обс = 20 мин.

3. Провести анализ работы в СМО при изменении одного условия в примере 2 — интенсивности приезда автомобилей на мойку до 6 автомобилей в час.

Рекомендации к решению задачи: здесь m = 2; λ = 6 ед. в час.; t_обс = 20 мин.

4. Рабочий обслуживает m станков. Поток требований на обслуживание пуассоновский с параметром λ станков в час. Время обслуживания одного станка подчинено экспоненциальному закону. Среднее время обслуживания одного станка равна μ минут.
Определить: 1) среднее число станков, ожидающих обслуживания, 2) коэффициент простоя станка, 3) коэффициент простоя рабочего.

Одноканальная СМО с неограниченной очередью

1. Булочная «Горячий хлеб» имеет одного контролера-кассира. В течение часа приходят в среднем 54 покупателя. Средняя» стоимость одной покупки составляет 7 руб. Среднее время обслуживания контролером-кассиром одного покупателя составляет 1 мин. Определим выручку от продажи, характеристики СМО и проведем анализ ее работы.

Рекомендации к решению задачи: здесь λ = 54 ед. в час.; μ = 60 ед. в час.

2. Интенсивность потока автомобилей на АЗС к колонке за бензином АИ-92 составляет 30 автомобилей в 1 ч, а среднее время заправки равно 5 мин. Проведем анализ работы системы массового обслуживания АЗС.

Рекомендации к решению задачи: здесь λ = 2.4 ед. в час.; t_обс = 20 мин.

3. В парикмахерской работает только один мужской мастер. Среднее время стрижки одного клиента составляет 20 мин. Клиенты в среднем приходят каждые 25 мин. Средняя стоимость стрижки составляет 60 руб. Как в первую смену с 9 до 15, так и во вторую — с 15 до 21, работают по одному мастеру. Провести анализ работы системы обслуживания.

Рекомендации к решению задачи: здесь λ = 30 ед. в час.; t_обс = 5 мин.
В качестве количества заявок в очереди можно указать, например, m = 4. тогда будут рассчитаны соответствующие вероятность появления данных заявок.

4. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.

Рекомендации к решению задачи: здесь λ = 0.4 ед. в час.; t_обс = 2 час, m = 2.
После получения решения единицы измерения «час» следует заменить на «сутки».

Тема 9. Моделирование систем массового обслуживания (СМО)

I. Одноканальная СМО с отказами.

Пример. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания для мойки автомобилей. Заявка — автомобиль, прибывший в момент, когда пост занят, — получает отказ в обслуживании. Интенсивность потока автомобилей 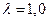(автомобиль в час). Средняя продолжительность обслуживания — 1,8 часа. Поток автомобилей и поток обслуживании являются простейшими. Определить в установившемся режиме характеристики системы.

Решение

1. Интенсивность потока обслуживания:

2. Относительная пропускную способность:

Следовательно, в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост автомобилей.

3. Абсолютная пропускная способность:

Следовательно, система способна осуществить в среднем 0,356 обслуживания автомобилей в час.

4. Вероятность отказа:

Следовательно, около 65% прибывших на пост автомобилей получат отказ в обслуживании.

II. Одноканальная СМО с ожиданием и ограниченной длиной очереди.

Пример. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно , т.е . Если все стоянки заняты, т. е. в очереди уже находится три автомобиля, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час. Определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

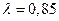
Решение

1. Параметр потока обслуживании автомобилей:

2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей 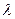и , т. е.

3. Вычислим финальные вероятности системы:

определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаивает), в данном примере она составляет 24,8%.

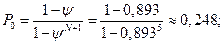
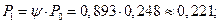
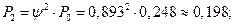
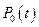
4. Вероятность отказа в обслуживании автомобиля:

5. Относительная пропускная способность поста диагностики:

6. Абсолютная пропускная способность поста диагностики: 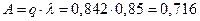(автомобиля в час)

7. Среднее число автомобилей, находящихся на обслуживании и в очереди (т.е. в системе массового обслуживания):

8. Среднее время пребывания автомобиля в системе:

часа

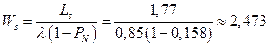
9. Средняя продолжительность пребывания заявки в очереди на обслуживание:

часа.

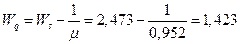
10. Среднее число заявок в очереди (длина очереди):

III. Одноканальная СМО с ожиданием и неограниченной длиной очереди.

Пример. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики неограничено. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность 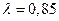(автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем равно 1,05 час. Определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

Решение

1.Параметр потока обслуживании автомобилей:

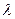
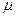
2. Приведенная интенсивность потока автомобилей определяется как отношение интенсивностей и , т. е.

3. Предельные вероятности системы:

и т.д. определяет долю времени, в течение которого пост диагностики вынужденно бездействует (простаивает), в данном примере она составляет 10,7%.

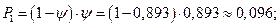
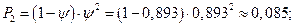
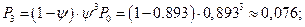
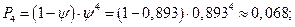
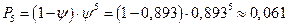
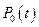
4. Среднее число автомобилей, находящихся в системе (на обслуживании и в очереди): 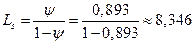ед.

5. Средняя продолжительность пребывания клиента в системе:

час.

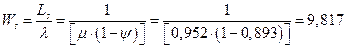
6. Среднее число автомобилей в очереди на обслуживание:

.

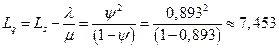
7. Средняя продолжительность пребывания автомобиля в очереди:

час.

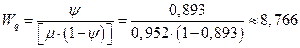
8. Относительная пропускная способность системы: 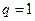, т. е. каждая заявка, пришедшая в систему, будет обслужена.

9. Абсолютная пропускная способность:

IV. Многоканальная СМО с отказами.

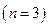
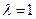
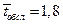
Пример. Пусть n-канальная СМО представляет собой вычислительный центр (ВЦ) с тремя взаимозаменяемыми ПЭВМ для решения поступающих задач. Поток задач, поступающих на ВЦ, имеет интенсивность задаче в час. Средняя продолжительность обслуживания час. Поток заявок на решение задач и поток обслуживания этих заявок являются простейшими. Определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

Решение

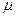
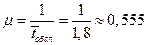
1. Параметр потока обслуживания: .

2. Приведенная интенсивность потока заявок: .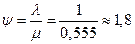

3. Предельные вероятности состояний: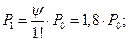

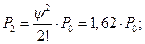
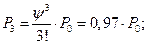
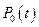
определяет долю времени, в течение которого (ВЦ) вынужденно бездействует (простаивает), в данном примере она составляет 18%.

4. Вероятность отказа в обслуживании заявки:

5. Относительная пропускная способность ВЦ:

6. Абсолютная пропускная способность ВЦ:

7. Среднее число занятых каналов – ПЭВМ:

V. Многоканальная СМО с ожиданием.

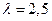
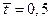
Пример. Механическая мастерская завода с тремя постами (каналами) выполняет ремонт малой механизации. Поток неисправных механизмов, прибывающих в мастерскую, — пуассоновский и имеет интенсивность механизма в сутки, среднее время ремонта одного механизма распределено по показательном у закону и равно сут. Предположим, что другой мастерской на заводе нет, и, значит, очередь механизмов перед мастерской может расти практически неограниченно. Определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.

Решение

1. Параметр потока обслуживаний:

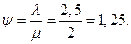
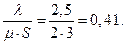
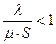
2. Приведенная интенсивность потока заявок: при этом Так как , то очередь не растет безгранично и в системе наступает предельный стационарный режим работы.

3. Вероятности состояний системы:

;

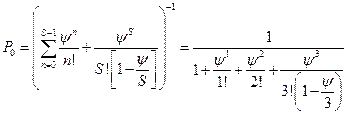
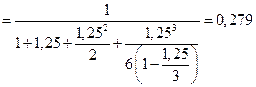
4. Вероятность отсутствия очереди у мастерской

5. Среднее число заявок в очереди на обслуживание

6. Среднее число находящихся в системе заявок:

7. Средняя продолжительность пребывания механизма в очереди на обслуживание

суток.

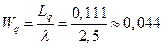
8. Средняя продолжительность пребывания механизма в мастерской (в системе)

суток.

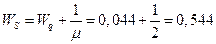
Контрольное задания №9

Вариант № 1.

Торговая фирма предполагает предоставлять своим клиентам возможность осуществлять заказ товаров по телефону. Для этой цели необходимо выделить и подготовить персонал, а также выбрать соответствующую мини-АТС с несколькими телефонными аппаратами. Порядок обслуживания должен быть следующим: если заказ поступает, когда все линии заняты, то абонент получает отказ. Если же в момент поступления заказа хотя бы одна линия свободна, то осуществляются переключение на эту линию и оформление заказа. Предполагаемая интенсивность входящего потока требований составляет 0,5 заказа/мин. Длительность же оформления заказа в среднем будет равна 5 мин.

Определите, какое минимальное количество каналов обслуживания необходимо, чтобы обеспечить выполнение условия стационарности МО, а также рассчитайте основные показатели работы СМО при использовании данного количества каналов.

Вариант 2.

Торговая фирма специализируется на продажах товаров для дома по методу direct marketing: потребители выбирают необходимые им товары по каталогу, а затем делают заказ товаров по телефону. Заказанные товары доставляют клиентам либо по почте, либо прямо на дом. Руководство фирмы приняло решение обновить существующую систему телефонной связи. Имеется возможность приобрести мини-АТС, обеспечивающую подключение 3 телефонных аппаратов, или мини-АТС, обеспечивающую подключение 5 телефонных аппаратов. Издержки, связанные с использованием этих мини-АТС таковы: издержки, связанные с эксплуатацией в минуту для первого случая 2,5 (у.е.), а для второго случая 4 (у.е.); издержки, связанные с простоем в минуту для первого случая 0,5 (у.е.), а для второго случая 1 (у.е.). Интенсивность входящего потока заказов клиентов составляет 1,2 заказа/мин. Интенсивность обслуживания требований равна 0,5 заказа/мин. Издержки, связанные с отказом в обслуживании, который происходит, когда все каналы связи заняты, составляет 45 у.е. Издержки, связанные с пребыванием требования в системе в единицу времени, не учитываются.

Определите основные параметры работы СМО при использовании мини-АТС, обеспечивающих подключение 3 и 5 телефонных аппаратов, и, используя функцию издержек в качестве критерия качества работы системы, осуществите выбор наиболее подходящей мини-АТС.

Вариант 3.

В универсальном магазине (в отделе самообслуживания) на выходе планируется разместить кассы сканирования для приема от покупателей денег за товары. Интенсивность потока покупателей равна 6 чел/мин. Интенсивность обслуживания составляет 1,4 чел/мин. Допустимая длина очереди не должна превышать 3 человек.

Определите, какое минимальное количество касс необходимо установить, чтобы выполнялось условие стационарности системы, а также рассчитайте основные показатели работы СМО при использовании данного количества касс.

Вариант 4.

Торговый центр располагается в 4-хэтажном здании. На его первом этаже находится склад, с которого товары доставляются на верхние этажи с помощью 2-х транспортных лифтов, а затем распределяются по отделам. На складе доставка к лифтам и погрузка в них товаров осуществляются двумя автопогрузчиками. Складирование товаров возле лифтов запрещено, поэтому если оба лифта заняты, автопогрузчики образуют очередь. Интенсивность входящего потока требований на погрузку товаров в лифты составляет 2 треб/час, а интенсивность обслуживания равна 1,5 треб/час. Дирекция торгового центра предполагает использовать только один лифт, а другой сделать резервным.

Определите, возможно ли использовать только один лифт для доставки товаров на этажи здания торгового центра, и рассчитайте основные показатели работы СМО при использовании реально необходимого количества лифтов.

Вариант 5.

Торговая фирма предполагает предоставлять своим клиентам возможность осуществлять заказ товаров по телефону. Для этой цели необходимо выделить и подготовить персонал, а также выбрать соответствующую мини-АТС с несколькими телефонными аппаратами. Порядок обслуживания должен быть следующим: если заказ поступает, когда все линии заняты, то абонент получает отказ. Если же в момент поступления заказа хотя бы одна линия свободна, то осуществляются переключение на эту линию и оформление заказа. Предполагаемая интенсивность входящего потока требований составляет 0,4 заказа/мин. Длительность же оформления заказа в среднем будет равна 4 мин.

Определите, какое минимальное количество каналов обслуживания необходимо, чтобы обеспечить выполнение условия стационарности МО, а также рассчитайте основные показатели работы СМО при использовании данного количества каналов.

Вариант 6.

Торговая фирма специализируется на продажах товаров для дома по методу direct marketing: потребители выбирают необходимые им товары по каталогу, а затем делают заказ товаров по телефону. Заказанные товары доставляют клиентам либо по почте, либо прямо на дом. Руководство фирмы приняло решение обновить существующую систему телефонной связи. Имеется возможность приобрести мини-АТС, обеспечивающую подключение 3 телефонных аппаратов, или мини-АТС, обеспечивающую подключение 4 телефонных аппаратов. Издержки, связанные с использованием этих мини-АТС таковы: издержки, связанные с эксплуатацией в минуту для первого случая 2 (у.е.), а для второго случая 3,5 (у.е.); издержки, связанные с простоем в минуту (у.е.) для первого случая 0,5, а для второго случая 1. Интенсивность входящего потока заказов клиентов составляет 1,2 заказа/мин. Интенсивность обслуживания требований равна 0,3 заказа/мин. Издержки, связанные с отказом в обслуживании, который происходит, когда все каналы связи заняты, составляет 35 (у.е.). Издержки, связанные с пребыванием требования в системе в единицу времени, не учитываются.

Определите основные параметры работы СМО при использовании мини-АТС, обеспечивающих подключение 3 и 4 телефонных аппаратов, и, используя функцию издержек в качестве критерия качества работы системы, осуществите выбор наиболее подходящей мини-АТС.

Вариант 7.

В универсальном магазине (в отделе самообслуживания) на выходе планируется разместить кассы сканирования для приема от покупателей денег за товары. Интенсивность потока покупателей равна 5 чел/мин. Интенсивность обслуживания составляет 1,5 чел/мин. Допустимая длина очереди не должна превышать 2 человек.

Определите, какое минимальное количество касс необходимо установить, чтобы выполнялось условие стационарности системы, а также рассчитайте основные показатели работы СМО при использовании данного количества касс.

Вариант 8.

Торговый центр располагается в 4-хэтажном здании. На его первом этаже находится склад, с которого товары доставляются на верхние этажи с помощью 2-х транспортных лифтов, а затем распределяются по отделам. На складе доставка к лифтам и погрузка в них товаров осуществляются двумя автопогрузчиками. Складирование товаров возле лифтов запрещено, поэтому если оба лифта заняты, автопогрузчики образуют очередь. Интенсивность входящего потока требований на погрузку товаров в лифты составляет 3 треб/час, а интенсивность обслуживания равна 2 треб/час. Дирекция торгового центра предполагает использовать только один лифт, а другой сделать резервным.

Определите, возможно ли использовать только один лифт для доставки товаров на этажи здания торгового центра, и рассчитайте основные показатели работы СМО при использовании реально необходимого количества лифтов.

Вариант 9.

Торговая фирма предполагает предоставлять своим клиентам возможность осуществлять заказ товаров по телефону. Для этой цели необходимо выделить и подготовить персонал, а также выбрать соответствующую мини-АТС с несколькими телефонными аппаратами. Порядок обслуживания должен быть следующим: если заказ поступает, когда все линии заняты, то абонент получает отказ. Если же в момент поступления заказа хотя бы одна линия свободна, то осуществляются переключение на эту линию и оформление заказа. Предполагаемая интенсивность входящего потока требований составляет 1 заказ/мин. Длительность же оформления заказа в среднем будет равна 3 мин.

Определите, какое минимальное количество каналов обслуживания необходимо, чтобы обеспечить выполнение условия стационарности МО, а также рассчитайте основные показатели работы СМО при использовании данного количества каналов.

Вариант 10.

Торговая фирма специализируется на продажах товаров для дома по методу direct marketing: потребители выбирают необходимые им товары по каталогу, а затем делают заказ товаров по телефону. Заказанные товары доставляют клиентам либо по почте, либо прямо на дом. Руководство фирмы приняло решение обновить существующую систему телефонной связи. Имеется возможность приобрести мини-АТС, обеспечивающую подключение 4 телефонных аппаратов, или мини-АТС, обеспечивающую подключение 5 телефонных аппаратов. Издержки, связанные с использованием этих мини-АТС таковы: издержки, связанные с эксплуатацией в минуту для первого случая 3 (у.е.), а для второго случая 4 (у.е.); издержки, связанные с простоем в минуту для первого случая 0,4 (у.е.), а для второго случая 1 (у.е.). Интенсивность входящего потока заказов клиентов составляет 1,2 заказа/мин. Интенсивность обслуживания требований равна 0,5 заказа/мин. Издержки, связанные с отказом в обслуживании, который происходит, когда все каналы связи заняты, составляет 45 (у.е.). Издержки, связанные с пребыванием требования в системе в единицу времени, не учитываются.

Определите основные параметры работы СМО при использовании мини-АТС, обеспечивающих подключение 4 и 5 телефонных аппаратов, и, используя функцию издержек в качестве критерия качества работы системы, осуществите выбор наиболее подходящей мини-АТС.