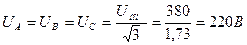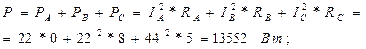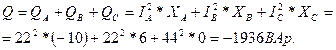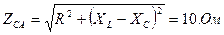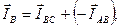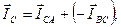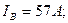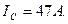Расчет цепей при соединении треугольником

Задача 2.В трехфазную сеть с UЛ = 380 В включен соединенный треугольником трехфазный асинхронный двигатель мощностью P = 5 кВт, КПД двигателя равен ηН = 90%, коэффициент мощности cos φ = 0,8. Определить фазные и линейные токи двигателя, параметры его схемы замещения RФ, XФ, построить векторную диаграмму. Включить ваттметры для измерения активной мощности и найти их показания.

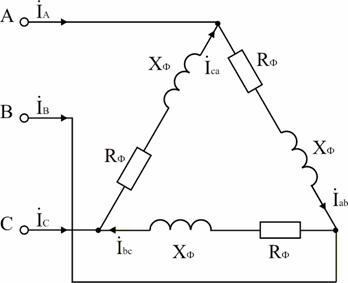
Анализ и решение задачи 2 Расчетная схема

Дано UЛ = 380 В Соед – Δ Pном = 5 кВт ή=0,8	Решение 1.Двигатель является активно-индуктивным потребителем энергии, его схема замещения приведена на рис. 2
Ia Ib Ic Iab Ibc Ica Rф Xф Рав Рвс Рсф	Рис. 2

2.Расчет активной мощности и токов, потребляемых двигателем из сети.

В паспорте двигателя указывается механическая мощность на валу; потребляемая активная мощность двигателя. Из формулы КПД

η= Рполез = Р ном

Pзатр = P_ном / η = 500 / 0.9 = 5560 Вт.

3.Для симметричной нагрузки, какой является двигатель,

P = 3 UФ IФ cos φ и IФ = P / (3 UФ cos φ).

IФ = 5560 / (3 · 380 · 0,8) = 6,09 А.

IЛ = √3· 6,09 = 1,73*6,09 = 10,54 А.

4.Расчет параметров схемы замещения двигателя.

ZФ = UФ / IФ = 380 / 6,09 = 62,4 Ом; RФ = ZФ cos φ = 62,4 · 0,8 = 49,9 Ом;

XФ = ZФ sin φФ = 62,4 · 0,6 = 37,4 Ом; cos φФ = cos φН = 0,8.

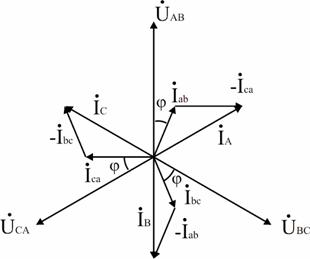
5.Построение векторной диаграммы.

Линейные напряжения строятся в виде симметричной звезды, они же являются в данном случае фазными напряжениями. Фазные токи отстают от напряжений на угол φФ, линейные токи строятся по фазным на основании уравнений, составленных по первому закону Кирхгофа:

ÍA = Íab — Íca; ÍB = Íbc — Íab; ÍC = Íca — Íbc.

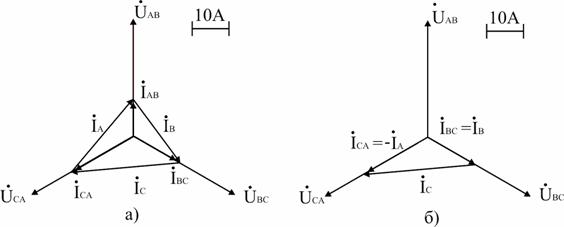
Векторная диаграмма показана на рис. 3

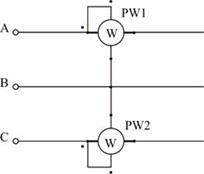
Схема включения ваттметров.

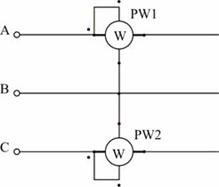
В трехпроводных сетях часто для измерения активной мощности применяется схема двух ваттметров, один из вариантов которой показан на рис. 4. Показания ваттметра определяются произведением напряжения, приложенного к его катушке напряжения, на ток в токовой катушке и косинус угла между ними:

P1 = U_AB I_A cos (Ú_AB ^ ÍA) = 380 · 10,54 · cos (φФ + 30°) = 1573 Вт;

P2 = U_CB I_C cos (Ú_CB ^ ÍC) = 380 · 10,54 · cos (φФ — 30°) = 3976 Вт.

Активная мощность трехфазной цепи равна алгебраической сумме показаний приборов: P = P1 + P2 = 1573 + 3976 = 5549 Вт.

Дополнительные вопросы к задаче 2

1. Можно ли этот двигатель включать в сеть с UЛ = 660 В?

Если при соединении треугольником двигатель имеет UЛ = 380 В, его можно использовать при Uсети = 660 В, соединив фазы звездой, т.к. при этом напряжение на его фазах UФ = 380 В.

2. Можно ли данный двигатель использовать в сети с UЛ = 380 В при соединении его обмоток звездой?

Можно, но напряжения на его фазах снижаются в √3 раз против номинального, что снижает допустимую мощность на валу; при номинальной нагрузке токи в обмотках двигателя будут больше номинальных.

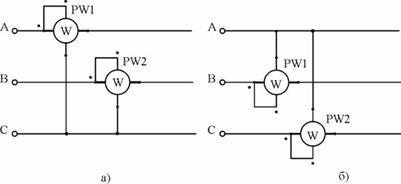
3. Как еще можно включить ваттметры для измерения активной мощности, потребляемой двигателем?

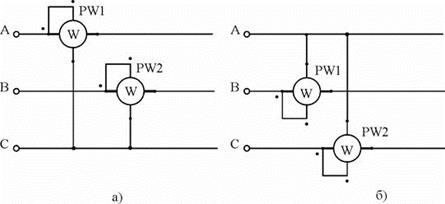
На рис. 5 показано еще два варианта подключения приборов по схеме двух ваттметров.

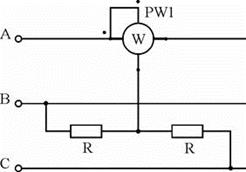
При симметричной нагрузке можно измерить мощность одним ваттметром, подключив его обмотку напряжения к соответствующему фазному напряжению сети (если доступна нейтральная точка) или создав искусственную точку (рис. 6), при этом прибор измеряет мощность одной фазы, мощность всей цепи Pцепи = 3 PW.

Задача 3. К источнику с UЛ = 220 В подключена соединенная треугольником осветительная сеть. Распределение нагрузки по фазам: PAB = 2200 Вт, PBC = 3300 Вт, PCA = 4400 Вт. Вычислить активную мощность, потребляемую схемой из сети, фазные и линейные токи приемников.

Дано: PAB = 2200 Вт, PBC = 3300 Вт, PCA = 4400 Вт Cosφ=1 Соед – Δ	Решение: 1.Активная мощность всей нагрузки равна сумме мощностей фаз: P = PAB + PBC + PCA = 2200 + 3300 + 4400 = 9900 Вт. 2.Расчет фазных токов. Т.к. осветительная сеть имеет cos φ = 1, для любой фазы IФ = PФ / UФ, поэтому:
Ia Ib Ic Iab Ibc Ica Rф Xф Рав Рвс Рсф	IAB = PAB/UAB = 2200/220 = 10 A IBC = PBC / UBC = 3300 / 220 =15 А; ICA = PCA / UCA = 4400 / 220 =20 А.

2.Аналитический расчет линейных токов выполняется на основании 1-го закона Кирхгофа; определим их графически, построив векторную диаграмму (рис. 7, а). 1см =10А. Тогда

I_AB = 10A/10= 1см; I_BC = 15/10 = 1.5см: I_CA= 20/10=2 см

Рис. 7.

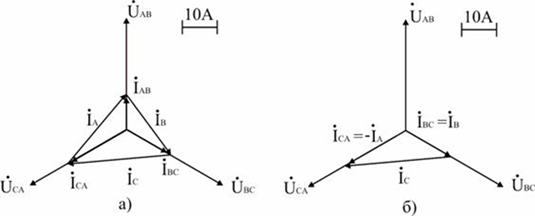
Измеряем линейкой Ia = 2.8см *10 =28 А

IB = 2.3 см *10 = 23А

IC = 2.7 см * 10= 27А

Дополнительные вопросы к задаче 3

1. Какие токи изменятся при перегорании ламп в фазе «AB»?

Ток IAB станет равен нулю; токи в фазах «BC» и «CA» останутся прежними, т.к. фазные напряжения не изменятся. Линейный ток IC, обусловленный токами IBC и ICA, также останется прежним, токи IA и IB будут равны по величине соответствующими фазными токами, т.к. по 1-му закону Кирхгофа теперь ÍA = -ÍCA, ÍB = -ÍBC (рис. 6.33, б).

2. Как изменятся токи в схеме при обрыве линейного провода «A»?

Режим работы фазы «BC» не изменяется, т.к. напряжение на ее зажимах остается номинальным. При обрыве линии «A» IA = 0; сопротивление фаз «AB» и «BC» соединены последовательно и включены на напряжение UBC, т.е. IAB = ICA = UBC / (RAB + RCA); напряжение UBC распределяется между ними пропорционально величинам сопротивлений.

Примеры решения задач на расчет цепей при соединении треугольником

Пример №1

Задача

В трехфазную сеть с U_Л = 380 В включен соединенный треугольником трехфазный асинхронный двигатель мощностью P = 5 кВт, КПД двигателя равен η_Н = 90%, коэффициент мощности cos φ_Н = 0,8. Определить фазные и линейные токи двигателя, параметры его схемы замещения R_Ф, X_Ф, построить векторную диаграмму. Включить ваттметры для измерения активной мощности и найти их показания.

Анализ и решение задачи

Двигатель является активно-индуктивным потребителем энергии, его схема замещения приведена на рис. 2

Расчет активной мощности и токов, потребляемых двигателем из сети.

В паспорте двигателя указывается механическая мощность на валу; потребляемая активная мощности двигателя

P = P_Н / η = 500 / 0.9 = 5560 Вт.

Для симметричной нагрузки, какой является двигатель,

P = 3 U_Ф I_Ф cos φ и I_Ф = P / (3 U_Ф cos φ).
I_Ф = 5560 / (3 · 380 · 0,8) = 6,09 А.
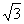
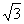
I_Л = I_Ф = · 6,09 = 10,54 А.

Расчет параметров схемы замещения двигателя.

Z_Ф = U_Ф / I_Ф = 380 / 6,09 = 62,4 Ом; R_Ф = Z_Ф cos φ = 62,4 · 0,8 = 49,9 Ом;
X_Ф = Z_Ф sin φ_Ф = 62,4 · 0,6 = 37,4 Ом; cos φ_Ф = cos φ_Н = 0,8.

Построение векторной диаграммы.

Линейные напряжения строятся в виде симметричной звезды, они же являются в данном случае фазными напряжениями. Фазные токи отстают от напряжений на угол φ_Ф, линейные токи строятся по фазным на основании уравнений, составленных по первому закону Кирхгофа:

Векторная диаграмма показана на рис. 3

Схема включения ваттметров.

В трехпроводных сетях часто для измерения активной мощности применяется схема двух ваттметров, один из вариантов которой показан на рисунке 4. Показания ваттметра определяются произведением напряжения, приложенного к его катушке напряжения, на ток в токовой катушке и косинус угла между ними:

Активная мощность трехфазной цепи равна алгебраической сумме показаний приборов: P = P₁ + P₂ = 1573 + 3976 = 5549 Вт.

На рисунке 5 показано еще два варианта подключения приборов по схеме двух ваттметров.

При симметричной нагрузке можно измерить мощность одним ваттметром, подключив его обмотку напряжения к соответствующему фазному напряжению сети (если доступна нейтральная точка) или создав искусственную точку (рис. 6), при этом прибор измеряет мощность одной фазы, мощность всей цепи P_цепи = 3 P_W.

Пример № 2

Задача

К источнику с U_Л = 220 В подключена соединенная треугольником осветительная сеть. Распределение нагрузки по фазам: P_AB = 2200 Вт, P_BC = 3300 Вт, P_CA = 4400 Вт. Вычислить активную мощность, потребляемую схемой из сети, фазные и линейные токи приемников.

Анализ и решение задачи

Активная мощность всей нагрузки равна сумме мощностей фаз:

P = P_AB + P_BC + P_CA = 2200 + 3300 + 4400 = 9900 Вт.

Расчет фазных токов. Т.к. осветительная сеть имеет cos φ = 1, для любой фазы I_Ф = P_Ф / U_Ф, поэтому:

Аналитический расчет линейных токов выполняется комплексным методом на основании 1-го закона Кирхгофа; определим их графически, построив векторную диаграмму (рис. 7, а)

Из диаграммы следует: I_A = 27,6 А; I_B = 22,8 А; I_C = 26,6 А.

Задание 1. Выполните расчет трехфазной цепи по условиям задачи 1.

В трехфазную сеть с U_Л = 380 В включен по схеме треугольник асинхронный двигатель, имеющий Z_Ф = 19 Ом, cos φ_Ф = 0,8. Найти линейные токи и активную мощность, потребляемую двигателем из сети.

Ответ: 34,6 А; 18,2 кВт.

Задание 2. Выполните расчет трехфазной цепи по условиям задачи 2.

Трехфазная печь включена в сеть с U_Л = 380 В по схеме треугольник. Найти линейный ток и мощность печи, если R_Ф = 10 Ом. Как изменятся линейный ток и мощность печи, если ее включить в ту же сеть по схеме звезда?

Ответ: 65,7 А; 43,2 кВт; 21,9 А; 14,4 кВт.

Контрольные вопросы

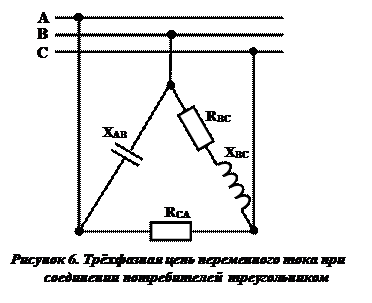
1. Начертите схему соединения потребителей по способу «треугольник» и подключения их к трехфазной сети.

2. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в несимметричной трехфазной цепи при их соединении треугольником?

3. Как определить общую активную Р, реактивную Q и полную S мощности электроприемников в симметричной трехфазной цепи при их соединении треугольником?

4. Как определить активную Рф, реактивную Qф и полную Sф мощности для отдельной фазы?

5. Запишите соотношение между фазными и линейными токами при соединении «треугольником»?

6. Запишите соотношение между фазными и линейными напряжениями при соединении «треугольником»?

7. Опишите, что произойдет в системе трехфазного питания при обрыве одного из линейных проводов.

Определяем полные сопротивления отдельных ветвей. 2 страница

В трехфазную четырехпроводную сеть включили звездой разные по характеру сопротивления. Значения сопротивлений и линейное напряжение приведены в таблице 4. Начертить схему цепи, определить полные сопротивления фаз, фазные токи, активную, реактивную и полную мощность отдельных фаз и всей цепи. Начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить графически числовое значение тока в нулевом проводе.

Указания к выполнению задачи №3.1:

Для решения данной задачи требуются знания учебного материала по теме «Трехфазные электрические цепи переменного тока», представление об особенностях соединения источников и потребителей, соотношениях между линейными и фазными напряжениями и токами при соединении в звезду, умения строить векторные диаграммы при симметричной и несимметричной нагрузках, а также в аварийных режимах. Данные для своего варианта взять из таблицы 4.

ПРИМЕР:

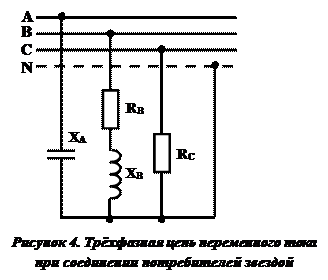
В трёхфазную четырёхпроводную сеть с частотой f = 50 Гц включили звездой несимметричную нагрузку:

— в фазу А – конденсатор с ёмкостным сопротивлением X_C = 10 Ом;

— в фазу В – активное сопротивление R = 8 Ом и индуктивное X_L= 6 Ом;

— в фазу С – активное сопротивление R = 5 Ом.

Линейное напряжение сети U_ном = 380 В.

Определить полные сопротивления фаз, фазные напряжения и токи; начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе; определить активную, реактивную и полную мощности, потребляемые цепью.

1. Определяем полное сопротивление каждой фазы:

;

; ; .

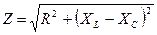
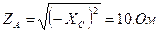
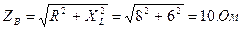
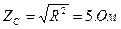
2. Определяем фазные напряжения:

3. Находим фазные токи:

, тогда ; ; .

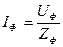
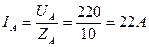
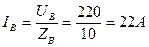
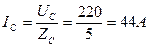
4. Построение векторной диаграммы:

Выбор масштаба: по напряжению: m_U = 100 В/см; по току: m_I = 10 A/см.

Первыми строят вектора фазных напряжений U_A, U_B, U_C, располагая их под углом 120 о друг относительно друга (рисунок 5). Вектор I_A опережает вектор U_A на угол 90 о (т.к. на реактивной емкостной нагрузке напряжение отстаёт от тока по фазе на 90 о ); вектор I_В отстаёт от вектора U_В на угол φ_В, который определяется из выражения 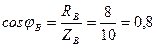φ_В = 36 о 50 ′ . Вектор I_С совпадает с вектором напряжения U_С (т.к. в фазе С содержится чисто активная нагрузка, а вектора напряжения и тока в этом случае имеют одинаковое направление). Ток в нулевом проводе равен геометрической сумме фазных токов.

Измерим длину вектора тока в нулевом проводе I_О: l_I »6,8см.

Тогда .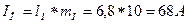

5. Определяем мощности, потребляемые цепью:

Знак минус показывает, что в цепи преобладает ёмкость.

.

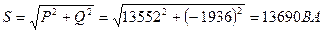
Задача 3.2

В трехфазную трехпроводную сеть включили треугольником разные по характеру сопротивления. Значения сопротивлений и линейное напряжение приведены в таблице 4. Начертить схему цепи, определить полные сопротивления фаз, фазные токи, активную, реактивную и полную мощность отдельных фаз и всей цепи. Начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить графически числовые значения линейных токов.

Указания к выполнению задачи №3.2:

Для решения данной задачи требуются знания учебного материала по теме «Трехфазные электрические цепи переменного тока», представление об особенностях соединения источников и потребителей, соотношениях между линейными и фазными напряжениями и токами при соединении в треугольник, умения строить векторные диаграммы при симметричной и несимметричной нагрузках, а также в аварийных режимах. Данные для своего варианта взять из таблицы 4.

В трёхфазную сеть с частотой f = 50 Гц включили треугольником несимметричную нагрузку (рис.6):

— в фазу АВ – конденсатор с ёмкостным сопротивлением X_C = 10 Ом;

— в фазу ВС – катушку с активным R = 4Ом и индуктивным сопротивлением X_L= 3 Ом;

— в фазу СА – активное сопротивление R=10 Ом.

Линейное напряжение сети U_ном = 220 В.

1. Определяем полное сопротивление каждой фазы:

;

;

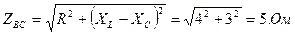
2. Определяем фазные токи и углы сдвига фаз:

,

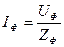
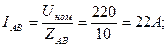
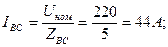
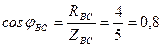
тогда φ_АВ = -90 о ;

откуда угол φ_ВС = 36 о 50 ′ ;

φ_СА = 0;

3. Построение векторной диаграммы: Выбор масштаба по напряжению: m_U = 80В/см; по току: m_I = 10 A/см.

Вектора фазных напряжений U_AВ, U_BС, U_CА располагают под углом 120 о друг относительно друга (рисунок 7). Под углом φ_АВ = —90 о к вектору напряжения U_AB откладываем вектор тока I_AB (т.к. в фазе чисто емкостная нагрузка); в фазе ВС вектор тока I_BС должен отставать от вектора напряжения U_BС на угол φ_ВС = 36 о 50 ′ , а в фазе СА вектор тока I_СА совпадает с вектором напряжения U_СА (т.к. в фазе СА содержится чисто активная нагрузка, а вектора напряжения и тока в этом случае имеют одинаковое направление).

Строим векторы линейных токов на основании уравнений:

Измерив длины векторов линейных токов, находим их значения, пользуясь масштабом

:

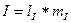
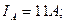
4. Определяем мощности, потребляемые цепью:

Вт;

.

.

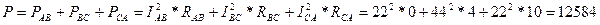
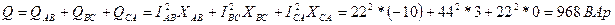
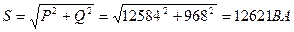
вариант	Фаза А	Фаза В	Фаза С	UЛ, В	вариант	Фаза АВ	Фаза ВС	Фаза СА	UЛ, В
R,Ом	XL ,Ом	XC,Ом	R,Ом	XL,Ом	XC,Ом	R,Ом	XL,Ом	XC,Ом	R,Ом	XL ,Ом	XC,Ом	R,Ом	XL,Ом	XC,Ом	R,Ом	XL,Ом	XC,Ом
12,7	25,4
12,7	25,4
12,7	80,5
82,7
62,8
80,5	12,7	25,4
40,5	80,5
5,5	6,3
82,7
25,4	12,7
25,4	12,7
6,35	12,7
12,7
6,35	12,7
12,7
12,7
12,7
82,7
2,5	4,6	7,5	82,7
80,5
37,5	34,5	20,2	2,5	4,6	7,5
25,4	12,7
80,5
25,4	12,7
5,5	6,3
17,3	17,3	17,3
80,5
80,5	7,5	2,5	4,6
82,7
2,5	4,6	7,5
28,3	17,3	17,3
80,5
25,4	24,7	12,7
12,7	25,4
2,5	4,6	7,5

Задача 4

Для питания пониженным напряжением частотой 50 Гц установлен трехфазный трансформатор номинальной мощностью S_НОМ, к которому подключена нагрузка с полной мощностью S₂, активной Р₂, при коэффициенте мощности соsφ_2. и коэффициенте нагрузки К_Н. Номинальные напряжения обмоток U_НОМ1 и U_НОМ2; номинальные токи в обмотках I_НОМ1 и I_НОМ2, токи в обмотках при фактической нагрузке I₁ и I₂, ЭДС в обмотках трансформатора Е₁ и Е₂. Коэффициент трансформации равен К. Число витков обмоток w₁ и w₂. Магнитный поток в магнитопроводе Ф_М. Магнитные потери Р_М=Р_Х, электрические потери Р_Э=Р_К. КПД трансформатора при номинальной нагрузке η_НОМ, при действительной нагрузке η, максимальное значение КПД η_М. Используя данные трансформатора, приведенные в таблице 5, и исходные данные, приведенные в таблице 7, определить все неизвестные величины. Ответить на вопрос из таблицы 6 в соответствии со своим вариантом.

Указания к выполнению задачи №4:

Для решения данной задачи необходимо знать устройство, принцип действия и соотношения между электрическими величинами трехфазных трансформаторов. Основными параметрами трансформаторов являются:

1. Номинальная мощность S_НОМ. Это полная мощность (в кВА), которую трансформатор, установленный на открытом воздухе, может непрерывно отдавать в течение срока службы (20-25 лет) при номинальном напряжении и при максимальной и среднегодовой температуре окружающего воздуха соответственно 40 и 5 о С.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет