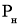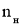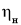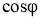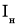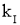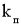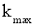Определение параметров схемы замещения асинхронного двигателя по каталожным данным

Асинхронный короткозамкнутый двигатель типа А13-37-6 имеет следующие технические данные:

— номинальная мощность Р_н = 500 кВт;

— номинальное напряжение U_lл = 6000 В;

— синхронная частота вращения п₀ = 1000 об/мин;

— номинальное скольжение s_н = 0,02 о.е.;

— коэффициент полезного действия в режиме номинальной мощ­ности (100%-я нагрузка) η_н = 93,5%;

— коэффициент мощности в режиме номинальной мощности cosφ_н=0,87о.е.;

— кратность пускового тока I_п/I_1н = k_i = 6 о.е.;

— кратность пускового момента М_п/М_н = k_п = 1 о.е.;

— кратность максимального момента М_mах/М_н = k_тах = 2,0 о.е.;

Эти данные позволяют определить параметры схемы замещения при следующих основных допущениях:

— магнитные и механические потери в двигателе составляют

— активные сопротивления статорной и роторной обмоток пола­гаются независящими от режима работы двигателя, т.е. эффек­ты вытеснения не учитываются.

Проведем расчет параметров Т-образной схемы замещения для короткозамкнутого асинхронного двигателя [12].

Определяется ток холостого хода асинхронного двигателя:

= = 17,25 A,

где I_1н – номинальный ток статора двигателя, А;

s_н = – номинальное скольжение, о.е.;

ω₀ – синхронная частота вращения, рад/с;

U_1н – номинальное фазное напряжение, В;

I₁₁ – ток статора двигателя при частичной загрузке:

= = 44,876 A,

cosφ_р* – коэффициент мощности при частичной загрузке, о.е.;

η_р* – КПД при частичной загрузке, о.е.;

р_*= Р/Р_н – коэффициент загрузки двигателя, о.е.;

Р — мощность двигателя при частичной загрузке, кВт.

Коэффициенты мощности и КПД при частичной загрузке в техни­ческой литературе приводятся редко, а для целого ряда серий электри­ческих машин такие данные в справочной литературе отсутствуют. Эти параметры можно определить, руководствуясь следующими соображе­ниями:

— современные асинхронные двигатели проектируются таким обра­зом, что наибольший КПД достигается при загрузке на 10-15% меньшей номинальной. Двигатели рассчитываются так потому, что большин­ство из них в силу стандартной дискретной шкалы мощностей работают с некоторой недогрузкой. Поэтому КПД при номинальной нагрузке и нагрузке р_* = 0,75 практически равны между собой, т.е. η_н = η_0,75.

— коэффициент мощности при той же нагрузке р_* = 0,75 сильно отличается от коэффициента мощности при номинальной нагрузке, причем это отличие в значительной степени зависит от мощности дви­гателя и для известных серий асинхронных двигателей с достаточной для практики точностью подчиняется зависимости, приведенной на рис. 3.2.

Из формулы Клосса определим выражение для расчета критиче­ского скольжения

= = 0,082,

где = = 1,024.

Значение коэффициента β находится в диапазоне 0,6 — 2,5(примем β=2).

Рисунок 3.2. Зависимость cosφ_0,75/ cosφ_н от мощности асинхронного двигателя

= = 17,226.

Тогда активное сопротивление ротора, приведенное к обмотке статора асинхронного двигателя:

= = 1.185 Ом.

Активное сопротивление статорной обмотки можно найти по следующему выражению:

= 1,024*1,185*2= 2,427 Ом.

Определим параметр γ, который позволяет найти индуктивное со­противление короткого замыкания Х_кн:

= = 12,03.

Очевидно, что при отрицательном подкоренном выражении первоначально принятое значение β необходимо изменить.

Тогда индуктивное сопротивление короткого замыкания

= 12,03*1,024*1,185 = 14,597 Ом.

Для того чтобы выделить из индуктивного сопротивления корот­кого замыкания Х_кн сопротивления рассеяния фаз статора Х_1σн и ротора Х’_2σн, воспользуемся соотношениями, которые справедливы для серийных асинхронных двигателей.

Индуктивное сопротивление рассеяния фазы роторной обмотки, приведенное к статорной, может быть рассчитано по уравнению

= 0,58*14,597/1,024 = 8,27 Ом.

Индуктивное сопротивление рассеяния фазы статорной обмотки может быть определено по следующему выражению:

= 0,42*14,597=6,13 Ом.

Согласно векторной диаграмме, ЭДС ветви намагничива­ния Е_т, наведенная потоком воздушного зазора в обмотке статора в но­минальном режиме, равна:

= =3166,16 В,

тогда индуктивное сопротивление контура намагничивания

= =183,55 Ом.

В результате расчетов были получены следующие параметры (табл.3.1).

Таблица 3.1. Параметры двигателя для Т-образной схемы замещения

R1, Ом	R’2, Ом	X1, Ом	X’2, Ом	Xµ, Ом	sк
2,427	1,185	6,13	8,27	183,55	0,082

Построим характеристики асинхронного двигателя [4].

Определим синхронную угловую скорость двигателя:

= = 104,67 рад/с.

Расчет естественной механической характеристики асинхронного двигателя произведем в соответствии с выражением:

.

Эффект вытеснения можно учесть, если при расчётах характеристик во всех выражениях умножить R₂′ на некоторую функцию k_r(s), сходящуюся при s→0 к единице, а при s→1 – к значению, обеспечивающему справочную величину пускового момента [12].

В качестве функции можно использовать полином вида k_r(s)=1+α⋅s β . Величина α определяется решением уравнения Клосса при s=1 из условия M(s=1) = k_пМ_п:

=

Величина β определяет форму механической характеристики и выбирается из условия получения требуемого индекса характеристики.

Механическая характеристика M(w) с учетом вытеснения тока приведена на рис. 3.3.

Рисунок 3.3. Естественная механическая характеристика асинхронного двигателя с учетом вытеснения тока

Определим дополнительные параметры двигателя.

• Момент критический двигательного режима

= = 10097 Н∙м;

= 0,0811;

• Номинальная скорость двигателя

= 102,57 рад/с;

• Номинальный момент двигателя

= 4874,72 Н∙м;

• Максимальный момент двигателя

= k_max∙M_н = 2∙4874,72 = 9749,44 Н∙м.

Определим зависимость тока ротора I₂’, приведенного к обмотке статора, от скольжения s:

.

График электромеханической характеристики I₂’(w) с учетом вытеснения тока приведен на рис. 3.4.

Рисунок 3.4. График электромеханической характеристики I₂’(w) с учетом

Номинальный ток ротора двигателя при номинальном скольжении

= 54,69 А.

Таким образом, анализ расчетов показывает, что контрольные точки, найденные в соответствии с каталожными данными двигателя, практически совпадают с рассчитанным графиком механической характеристики асинхронного двигателя, поэтому методику определения параметров схемы замещения асинхронного двигателя по его каталожным данным можно считать приемлемой.

Исследование методов расчета параметров схемы замещения асинхронного двигателя по данным каталога производителя

Рубрика: Технические науки

Дата публикации: 13.05.2020 2020-05-13

Статья просмотрена: 143 раза

Библиографическое описание:

Мясовский, В. А. Исследование методов расчета параметров схемы замещения асинхронного двигателя по данным каталога производителя / В. А. Мясовский. — Текст : непосредственный // Молодой ученый. — 2020. — № 20 (310). — С. 127-133. — URL: https://moluch.ru/archive/310/69984/ (дата обращения: 25.03.2021).

Работа представляет собой исследование методов расчета параметров схемы замещения асинхронного двигателя по данным каталога производителя и анализ результатов моделирования по этим расчетам в MATLAB Simulink.

Ключевые слова: расчет, параметры схемы замещения, асинхронный двигатель, каталожные данные, MATLAB Simulink.

Асинхронные двигатели получили широкое применение во всех отраслях промышленности, поскольку они обладают относительно невысокой стоимостью и намного проще в обслуживании, чем двигатели постоянного тока. Вследствие этого для изучения поведения асинхронных двигателей существуют различные способы моделирования процессов, происходящих при их работе. Конечно, есть более наглядный и реальный способ изучения — использование лабораторных стендов в учебных заведениях. Однако пользование лабораторными стендами ограничено по времени, поскольку их в учебном заведении не бесчисленное количество и при проведении работ необходимо присутствие ответственного лица — преподавателя или лаборанта. Также моделирование позволяет изучить процессы, происходящие в любом желаемом двигателе, для расчета параметров схемы замещения которого необходимы только каталожные данные, предоставляемые производителем. В данной статье и будут рассмотрены различные способы расчета параметров схемы замещения асинхронных двигателей.

Как было сказано ранее, параметры схемы замещения, необходимые для моделирования, возможно рассчитать при помощи каталожных данных двигателя, предоставляемых производителями асинхронных двигателей. Данные способы не претендуют на высокую точность результатов моделирования, но позволяют довольно достоверно оценить даже переходные процессы в двигателях. Конечно, существуют более точные способы расчета, которые позволяют производить более точное моделирование, однако они требуют большего количества данных асинхронной машины, которые обычно не предоставляются современными производителями. Например, в справочнике [2] имеются все параметры схемы замещения, однако данный справочник описывает определенную серию двигателей советского производства, которые не всегда могут являться исследуемым двигателем, хотя и обладают высокой распространенностью на территории России.

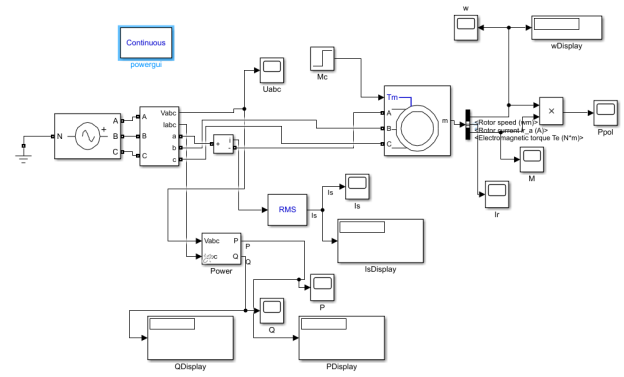
Для осуществления моделирования используется компьютерная программа MATLAB Simulink. Данная программа с огромным количеством прикладных пакетов позволяет проводить исследования в различных сферах науки от нейронных сетей до моделирования финансовых прогнозов. Также есть дополнительный пакет SimPowerSystems содержащий в себе большое количество готовых блоков для разрабатывания схем моделирования работы электрических систем. Схема моделирования представлена на рисунке ниже.

Рис. 1. Схема моделирования в MATLAB

Исследуемым двигателем был выбран двигатель высокой мощности и высокого питающего напряжения по следующим причинам:

1. Двигатели высокой мощности невозможно исследовать на лабораторных стендах ввиду их отсутствия, поскольку они являются очень дорогими устройствами.
2. Проверить возможность расчета параметров схемы замещения по каталожным данным достоверно отображать поведение двигателей при моделировании, так как обычно этими методами исследуются двигатели средней мощности и питанием напряжения от сети 380 Вольт.

Каталожные параметры исследуемого двигателя, питающегося от сети напряжением U_лн=10000 Вольт и частотой f₁=50 Герц приведены в таблице ниже:

Паспортные данные асинхронного двигателя Siemens 1RA4 452–4HE80

, кВт

, об/мин

, %

, о.е.

, А

, о.е.

, о.е.

, о.е.