Laboratornye_raboty_SoproMat

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования «Казанский национальный исследовательский технологический университет»

(ФГБОУ ВПО «КНИТУ»)

Составители: проф. А.Х.Валиуллин, проф. М.Н.Серазутдинов, доц. С.Г.Сидорин, доц. Ф.С.Хайруллин

Лабораторные работы по курсу сопротивления материалов:

Метод. указания / Казан. нац. исслед-кий технол. ун-т; Сост.: А.Х.Валиуллин, М.Н.Серазутдинов, С.Г.Сидорин, Ф.С.Хайруллин.

Казань, 2011, 64 с.

Методические указания предназначены для подготовки и выполнения лабораторных работ.

Рекомендуются студентам всех специальностей и форм обучения всех, изучающим дисциплину «Сопротивление материалов».

Подготовлены на кафедре теоретической механики и сопротивления материалов

Печатаются по решению методической комиссии цикла общепрофессиональных дисциплин

Рецензенты: проф. Лашков В.А. доц. Петухов Н.П.

Лабораторная работа 1

ИСПЫТАТЕЛЬНЫЕ МАШИНЫ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ

Цель работы . Изучить устройство механической испытательной машины SZ -10-1 и испытательного стенда МИ-40, ознакомиться с устройством и принципами работы механического рычажного тензометра Гуггенбергера, тензорезистора и измерительного моста.

Содержание работы . Любая лабораторная работа по сопротивлению материалов связана с механическим испытанием (нагружением) образца материала или элемента конструкции и, как правило, с измерением деформаций. Нагружение образцов и деталей осуществляется на специальных испытательных машинах, в лабораторной практике используются машины с усилиями от сотен килограммов до 10 — 20

тонн (100 – 200 кН).

Испытательная машина состоит из четырех обязательных частей: нагружающего механизма, силоизмерительного устройства, опорнозахватных приспособлений и станины. Большинство машин имеет также механизм записи диаграммы «деформация — усилие».

По типу нагружающего устройства испытательные машины получили следующие названия: рычажные, гидравлические, механические (винтовые). Чаще встречаются механизмы рычажного нагружения, которые применяются в машинах для испытания на длительную прочность, ползучесть и релаксацию. Распространены машины, в которых усилие вызывается вывинчиванием невращающегося винта из гайки, приводимой во вращение вручную или от электродвигателя. Машины, рассчитанные на большие усилия (более 30 тонн), имеют в качестве нагружающего устройства чаще всего гидравлический цилиндр с поршнем. Усилие создается за счет повышения давления жидкости под поршнем.

Силоизмерительное устройство кроме понятного из его названия назначения служит и для записи диаграммы испытания образца. Обычно в машинах используются маятниковые силоизмерители.

Опорно-захватные приспособления (захваты, зажимы для кручения, растяжения, столики для сжатия, опоры для изгиба и т.п.) служат

для закрепления образца или детали в испытательной машине. Перечисленные устройства крепятся на станине машины.

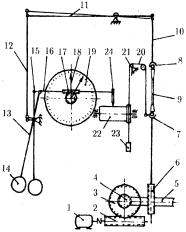
На рис. 1 схематически показано устройство механической разрывной машины.

Электродвигатель 1 приводит во вращение червяк 2, который при необходимости можно вращать вручную с помощью рукоятки, затем червячное колесо 3 и второй червяк 4. От червяка 4 вращение передается червячному колесу 5, которое имеет внутреннюю нарезку и является гайкой винта 6. При вращении гайки винт, вращение которого исключено, двигается поступательно вверх или вниз. С верхним концом винта соединен нижний захват 7. В захватах 7 и 8 закрепля-

Рис.1 Схема разрывной машины ется образец 9, который при движении винта вниз растягивается.

Рычажно — маятниковый силоизмеритель работает следующим образом. Верхний захват 8 с помощью тяги 10 подвешен шарнирно к правому концу рычага 11, с которым также шарнирно с помощью тяги 12 связан ломаный рычаг 13 с грузом 14 на конце (маятник). Усилие, действующее на образец, через тягу 10 опускает правый конец рычага 11, и вся рычажная система выходит из равновесия; левый конец рычага поднимается вверх, через тягу 12 поворачивая по часовой стрелке маятник. В результате рычажная система уравновешивается в новом положении, отклонение маятника будет прямо пропорционально величине усилия в образце, это и используется для измерения усилия. Вместе с маятником поворачивается толкатель 15, который перемещает рейку 16, а та, в свою очередь, поворачивает зубчатое колесо 17, на одной оси с которым насажена стрелка 18. Угол поворота стрелки в результате оказывается пропорциональным величине усилия. Шкала

19 тарируется в килограммах. Изменение шкал достигается установкой грузов 14.

Для автоматической записи диаграммы «деформация — усилие» к нижнему захвату 7 прикреплена нить 20, перекинутая через блоки 21 (один из которых находится на верхнем захвате), далее через шкив барабана 22, к концу нити привязан грузик 23. При изменении расстояния между захватами груз 23 поднимается или опускается, поворачивая барабан 22. На рейке 16 укреплен карандаш 24, который вычерчивает на бумаге барабана график, причем перемещение карандаша вдоль образующей барабана пропорционально усилию, а перемещение по окружности барабана — изменению расстояния между захватами, или деформации образца.

Машина может иметь сменные захваты для закрепления образцов

Описание испытательной установки

В настоящей лабораторной работе проводятся электрические испытания диэлектрических перчаток, бот, галош, слесарно-монтажного инструмента с изолирующими рукоятками, изолирующей штанги и указателя напряжения с газоразрядной лампой. Схема установки для электрических испытаний представлена на рис. 1.

Испытательная установка включает в себя испытательное поле, огражденное металлической сеткой и пульты управления ПУ-1 и ПУ-2.

У двери установлены блок-контакты, что обеспечивает невозможность подачи напряжения на испытываемые изделия при открытой двери, а также красная сигнальная лампа, указывающая о том, что дверь в испытательное поле закрыта.

а)	б)
в)	г) д)
Рис. 2. Расположение испытываемых изделий: а) диэлектрические перчатки; б) диэлектрические боты; в) слесарно-монтажный инструмент; г) изолирующая штанга; д) указатель напряжения

Изделие, подвергающееся электрическим испытаниям, устанавливается на испытательном поле (рис. 2). При испытаниях диэлектрических резиновых перчаток, бот, галош изделие располагается в металлическом баке с водой (рис.2, а, б), причем вода заливается в перчатки, боты, галоши. Уровень воды как снаружи, так и внутри изделий должен быть на 50 мм ниже верхнего края перчаток, отворот бот и на 20 мм ниже бортов галош. Слесарно-монтажный инструмент с изолирующими рукоятками (рис. 2в) погружается изолированной частью в ванну с водой так, чтобы вода не дохо­дила до края изоляции на 10 мм. При испытаниях изолирующей штанги, указателя напряжения изделия подвешивается к изолятору (рис. 2, г, д) и к временному электроду присоединяется высоковольтный провод испытательной установки.

При испытании диэлектрических перчаток, бот, галош, слесарно-монтажного инструмента с изолирующими рукоятками используются пульт управления ПУ-1. В этом случае используется испытательный трансформатор Т2, переключатель S3 должен находиться в положении «15 кВ». После включения автомата АП-50-1 (переключатель S1 на схеме рис. 1) загорается сигнальная лампа зеленая HI, указывающая на наличие напряжения, и красная лампа Н2, сигнализирующая о закрытом положении двери. Включением кнопки S5 (черного цвета) подается напряжение на обмотку реле К, которое срабатывает и замыкает контакты Kl, K2, КЗ. При этом загорается красная лампа НЗ на пульте управления ПУ-1, сигнализирующая о срабатывании реле, блокируется кнопка S5 и подается напряжение на обмотку автотрансформатора Т1, находящегося на лицевой панели ПУ-1. Вращением ручки автотрансформатора по часовой стрелке устанавливается необходимое испытательное напряжение на изделия. Показания фиксируются по шкале прибора, установленного на первичной стороне испытательного трансформатора Т2 и отградуированного в киловольтах. При наличии дефекта в изделии загорается газоразрядная лампа VT, находящаяся на ПУ-1. В этом случае необходимо прекратить подачу напряжения на изделие нажатием кнопки S4 и его заменить. При отсутствии пробоя или перекрытия изоляции изделия лампа VT не горит и ток, проходящий через изделие, регистрируется миллиамперметром мА при нажатом положении кнопки S6.

При испытаниях изолирующей штанги, указателя напряжения используется пульт управления ПУ-2, в качестве которого используется аппарат испытания изоляции АИИ-70. В этом случае ис­пользуется испытательный трансформатор Т4 (рис. 1 б) и переключатель S3 устанавливается в положение «70 кВ». Для подачи испытательного напряжения на изделие включается переключатель S1 и кнопка S5. При этом должны загореться сигнальные лампы HI, НЗ (на пульте управления ПУ-1), Н2 (на двери) и Н4 зеленого цвета на пульте управления ПУ-2. Далее включается автомат АП-50-1 (переключатель S2 нa рис.1, б), загорается красная сигнальная лампа Н5 и напряжение пода­ется на обмотку автотрансформатора Т3, ручкой регулятора напряжения устанавливается необходимое испытательное напряжение на изделие. Ток, протекающий через изделие, в этом случае не регистрируется. Работа проводится в диэлектрических перчатках.

Рабочее задание

1. Изучить и выписать нормы и сроки испытания электрозащитных средств, находящихся в эксплуатации (таблица 1).

2. Ознакомиться с расположением элементов испытательной установки и изделий на испытательном поле.

3. Провести электрические испытания диэлектрических перчаток, бот, галош, слесарно-монтажного инструмента по схеме рис. 1, а.

ЛАБОРАТОРНЫЕ РАБОТЫ ПО КУРСУ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ. Методические указания

1 Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический университет» (ФГБОУ ВПО «КНИТУ») ЛАБОРАТОРНЫЕ РАБОТЫ ПО КУРСУ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ Методические указания

2 УДК Составители: проф. А.Х.Валиуллин, проф. М.Н.Серазутдинов, доц. С.Г.Сидорин, доц. Ф.С.Хайруллин Лабораторные работы по курсу сопротивления материалов: Метод. указания / Казан. нац. исслед-кий технол. ун-т; Сост.: А.Х.Валиуллин, М.Н.Серазутдинов, С.Г.Сидорин, Ф.С.Хайруллин. Казань, 2011, 64 с. Методические указания предназначены для подготовки и выполнения лабораторных работ. Рекомендуются студентам всех специальностей и форм обучения всех, изучающим дисциплину «Сопротивление материалов». Подготовлены на кафедре теоретической механики и сопротивления материалов Печатаются по решению методической комиссии цикла общепрофессиональных дисциплин Рецензенты: проф. Лашков В.А. доц. Петухов Н.П. 3

3 Лабораторная работа 1 ИСПЫТАТЕЛЬНЫЕ МАШИНЫ И ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ Цель работы. Изучить устройство механической испытательной машины SZ-10-1 и испытательного стенда МИ-40, ознакомиться с устройством и принципами работы механического рычажного тензометра Гуггенбергера, тензорезистора и измерительного моста. Содержание работы. Любая лабораторная работа по сопротивлению материалов связана с механическим испытанием (нагружением) образца материала или элемента конструкции и, как правило, с измерением деформаций. Нагружение образцов и деталей осуществляется на специальных испытательных машинах, в лабораторной практике используются машины с усилиями от сотен килограммов до тонн ( кн). Испытательная машина состоит из четырех обязательных частей: нагружающего механизма, силоизмерительного устройства, опорнозахватных приспособлений и станины. Большинство машин имеет также механизм записи диаграммы «деформация — усилие». По типу нагружающего устройства испытательные машины получили следующие названия: рычажные, гидравлические, механические (винтовые). Чаще встречаются механизмы рычажного нагружения, которые применяются в машинах для испытания на длительную прочность, ползучесть и релаксацию. Распространены машины, в которых усилие вызывается вывинчиванием невращающегося винта из гайки, приводимой во вращение вручную или от электродвигателя. Машины, рассчитанные на большие усилия (более 30 тонн), имеют в качестве нагружающего устройства чаще всего гидравлический цилиндр с поршнем. Усилие создается за счет повышения давления жидкости под поршнем. Силоизмерительное устройство кроме понятного из его названия назначения служит и для записи диаграммы испытания образца. Обычно в машинах используются маятниковые силоизмерители. Опорно-захватные приспособления (захваты, зажимы для кручения, растяжения, столики для сжатия, опоры для изгиба и т.п.) служат 4

4 для закрепления образца или детали в испытательной машине. Перечисленные устройства крепятся на станине машины. На рис. 1 схематически показано устройство механической разрывной машины. Электродвигатель 1 приводит во вращение червяк 2, который при необходимости можно вращать вручную с помощью рукоятки, затем червячное колесо 3 и второй червяк 4. От червяка 4 вращение передается червячному колесу 5, которое имеет внутреннюю нарезку и является гайкой винта 6. При вращении гайки винт, вращение которого исключено, двигается поступательно вверх или вниз. С верхним концом винта соединен нижний захват 7. В захватах 7 и 8 закрепляется образец 9, который при дви- Рис.1 Схема разрывной машины жении винта вниз растягивается. Рычажно — маятниковый силоизмеритель работает следующим образом. Верхний захват 8 с помощью тяги 10 подвешен шарнирно к правому концу рычага 11, с которым также шарнирно с помощью тяги 12 связан ломаный рычаг 13 с грузом 14 на конце (маятник). Усилие, действующее на образец, через тягу 10 опускает правый конец рычага 11, и вся рычажная система выходит из равновесия; левый конец рычага поднимается вверх, через тягу 12 поворачивая по часовой стрелке маятник. В результате рычажная система уравновешивается в новом положении, отклонение маятника будет прямо пропорционально величине усилия в образце, это и используется для измерения усилия. Вместе с маятником поворачивается толкатель 15, который перемещает рейку 16, а та, в свою очередь, поворачивает зубчатое колесо 17, на одной оси с которым насажена стрелка 18. Угол поворота стрелки в результате оказывается пропорциональным величине усилия. Шкала 5

5 19 тарируется в килограммах. Изменение шкал достигается установкой грузов 14. Для автоматической записи диаграммы «деформация — усилие» к нижнему захвату 7 прикреплена нить 20, перекинутая через блоки 21 (один из которых находится на верхнем захвате), далее через шкив барабана 22, к концу нити привязан грузик 23. При изменении расстояния между захватами груз 23 поднимается или опускается, поворачивая барабан 22. На рейке 16 укреплен карандаш 24, который вычерчивает на бумаге барабана график, причем перемещение карандаша вдоль образующей барабана пропорционально усилию, а перемещение по окружности барабана — изменению расстояния между захватами, или деформации образца. Машина может иметь сменные захваты для закрепления образцов различной толщины, съемные опоры для испытания на изгиб, устройство обратного хода (реверсор) для испытания на сжатие. 3 Рис. 2 Испытательный стенд МИ-40 Универсальный испытательный стенд МИ-40 предназначен для проведения испытаний материалов на растяжение, сжатие, кручение, кручение с растяжением, кручение со сжатием. Машина используется совместно с ЭВМ. В состав машины входят (рис. 2): нагружающее устройство, блок управления, захваты, соединительные кабели. Нагружающее устройство состоит из станины 1, неподвижной 2 и подвижной 3 траверс, активного 4 и пассивного 5 охватов, пульта управления 6. При испытаниях на сжатие вместо захватов устанавливаются столики, при проведении испытаний на кручение и комбинированных испытаниях устанавливаются специальные захваты. Управление работой стенда и связь с ЭВМ производится с помощью блока управления. Машина обеспечивает построение графиков

6 зависимости деформаций от усилий и моментов на дисплее ЭВМ. Наибольшая предельная нагрузка на растяжение-сжатие 40 кн, наибольший предельный момент на кручение 200 кн м. Деформации, возникающие в испытуемых образцах, обычно очень малы: абсолютные деформации измеряются микронами и сотыми долями миллиметра, а относительные — десятыми и сотыми долями процента. Для измерения таких малых деформаций применяются специальные высокочувствительные приборы — тензометры. Их можно разделить на две группы: механические и электрические l h 4 l h h 2 4 h 1 Рис. 3 Рычажный тензометр Схема механического рычажного тензометра Гуггенбергера показана на рис. 3. К корпусу 1 жестко прикреплена неподвижная призма 2, в корпусе прибора имеется двугранный паз, на ребро которого опирается подвижная призма 3. Расстояние между призмами в исходном положении называется базой тензометра. Заодно с призмой 3 выполнен рычаг 4, который с помощью тяги 5 шарнирно связан со стрелкой 6, конец которой перемещается вдоль шкалы 7. Прибор прикрепляется к образцу с помощью струбцины. При растяжении (сжатии) образца подвижная призма поворачивается, вместе с ней поворачивается рычаг 4, тяга 5 отклоняется, поворачивая стрелку 6. Из схемы видно, что если удлинение образца на базе l составляет Δl, то стрелка прибора отклоняется на ΔТ, причем T h2 h4 k. l h1 h3 Отношение приращения показания прибора к величине измеряемой деформации называется коэффициентом увеличения тензометра. В обычном исполнении у тензометра Гуггенбергера l = 20 мм, k =

7 Примерно также устроены и другие механические тензометры (Морозова-Ильина, Бояршинова). В тензометре Аистова для измерения используется микрометрический винт. К электрическим тензометрам относятся приборы, в которых деформация преобразуется в какую-нибудь электрическую величину, измеряемую электроприборами: омическое сопротивление, емкость, индуктивность и т.д. Наибольшее распространение получили электрические тензометры, использующие в качестве воспринимающего устройства тензодатчики сопротивления (тензорезисторы). Рис. 4 Тензорезистор Тензорезистор представляет собой решетку из проволоки константана, нихрома или манганина диаметром 0,020,04 мм, приклеенную к подложке (из бумаги или пленки), с выводными проводами большего сечения (рис. 4). Тензодатчик наклеивается на исследуемую деталь и деформируется вместе с ней. При этом изменяются длина и поперечное сечение проволоки, что приводит к изменению омического сопротивления тензодатчика. Опыт показывает, что относительное изменение сопротивления тензодатчика прямо пропорционально относительной деформации: R K T, R где R — первоначальное сопротивление тензодатчика, R приращение сопротивления тензодатчика, — относительная деформация, K Т — коэффициент пропорциональности, называемый коэффициентом тензочувствительности; для наиболее распространенных проволочных тензодатчиков базой мм К Т 2. Таким образом, измерение деформации сводится к измерению сопротивления тензодатчика, для чего используются электрические мосты постоянного и переменного тока. На рис. 5 показана принципиальная схема измерительного моста. Мост состоит из источника питания, четырех плеч с сопротивлениями R 1, R 2, R 3, R 4. Одним из плеч моста является сопротивление рабочего или активного тензодатчика, пусть R 1 = R А. К одной диагонали моста подключен источник питания, к другой — гальванометр. Перед 8

8 измерением мост балансируется так, чтобы в измерительной диагонали ток был равен нулю, что достигается при выполнении соотношения R 1 R 3 = R 2 R 4. Обычно в качестве сопротивления R 2 берут компенсационный датчик, сопротивление которого равно сопротивлению рабочего датчика: R 2 = R 1 = R А. Компенсационный датчик приклеивается на недеформируемую пластинку из исследуемого материала и помещается вблизи активного, чтобы возможные изменения температуры действовали на оба датчика. Он компенсирует температурные изменения сопротивления, отсюда и Рис. 5 Измерительный мост его название компенсационный. Тогда из приведенного выше соотношения следует R 4 = R 3 = R. Обычно два плеча моста с рабочим и компенсационным датчиками делаются выносными, а сопротивления R 3 и R 4 монтируются внутри прибора, одно из них, например R 4, является переменным, т.е. реохордом, шкала реохорда градуируется не в омах, а непосредственно в единицах относительной деформации. Измерение статической деформации выполняется так. Вначале при нулевой деформации производится балансировка моста изменением сопротивления реохорда и записывается показание шкалы реохорда, затем то же повторяется после деформирования объекта, деформация находится как разность показаний двух измерений. В приборе ЦТМ-5 балансировка измерительного моста выполняется автоматически, показания реохорда высвечиваются цифрами на экране. Деформации можно измерить и непосредственно гальванометром моста, если проградуировать шкалу гальванометра в единицах деформации, при этом шкала прибора будет линейной, т.е. равномерной. Действительно, при деформировании объекта сопротивление рабочего датчика изменяется на величину R А, балансировка моста нарушается, и в измерительной диагонали пойдет ток I r R 2R RA RA A. 9

9 Как видно, сила тока I r моста прямо пропорциональна изменению сопротивления активного тензодатчика, и, следовательно, измеряемой деформации. Описанный метод носит название метода непосредственного измерения. На практике этот метод реализуется в более сложных установках и применяется для измерения и непрерывной записи деформации в быстро протекающих процессах. Эти установки рассчитаны на одновременное подключение нескольких датчиков (имеются установки на 100 и даже 1000 точек). Контрольные вопросы 1. Опишите принципиальную схему устройства механической испытательной машины SZ Как устроен нагружающий механизм испытательной машины SZ-10-1? 3. Как работает силоизмерительное устройство испытательной машины SZ-10-1? 4. Каково устройство опорно-захватных приспособлений? 5. Как устроен и работает рычажный тензометр Гуггенбергера? 6. Как устроен и работает тензорезистор? 7. Описать принципиальную схему измерительного моста. Лабораторная работа 2 ИСПЫТАНИЕ МЕТАЛЛОВ НА РАСТЯЖЕНИЕ Цель работы: испытать образцы, изготовленные из разных металлов, на растяжение и определить их основные механические характеристики. Образцы для испытаний: форма и размеры образца круглого поперечного сечения соответствуют ГОСТ (рис. 6). Испытательные машины: испытания проводятся на универсальных разрывных машинах и испытательных стендах. Содержание работы. Для изучения свойств материала под нагрузкой обычно производят лабораторные испытания образцов, подготовленных из этих материалов, на специальных испытательных машинах. Эти испытания проводятся для определения числовых характеристик, 10

10 позволяющих оценить прочность и пластичность материала. Такие характеристики называются механическими. d 0 l 0 Рис. 6. Образец для испытания. Особенно важное значение имеют испытания материалов на растяжение, при которых наиболее полно выявляются свойства материалов. В работе определяются характеристики прочности и пластичности материала при растяжении. Образец закрепляется в захватах машины и подвергается деформированию вплоть до разрушения. При этом зависимость, между растягивающей силой F и величиной продольной деформации l записывается в виде графика (рис. 7), который называется машинной диаграммой растяжения материала. F К E S В А С D FВ FР FП FУ FТ О ΔlОСТ К 1 ΔlУ Δl ΔlПОЛН разр ΔlОСТ разр ΔlПОЛН ΔlУ разр Рис. 7. Машинная диаграмма пластичной стали 11

11 Для изучения свойств материала удобнее пользоваться диаграммой растяжения, устанавливающей связь между нормальным напряжением σ и деформацией ε, которую называют условной диаграммой растяжения. При построении условной диаграммы растяжения используют формулы F l,, A 0 где F растягивающая сила, А 0 первоначальная площадь поперечного сечения образца, l 0 длина образца, l удлинение. Величины F и l берутся из экспериментально полученной диаграммы растяжения. Рассмотрим диаграмму растяжения образца из малоуглеродистой стали Ст.3 (рис. 8). σ E l 0 S В А С D σв σр σп σ У σт О Рис. 8. Условная диаграмма растяжения пластичной стали S 2 ε На этой диаграмме необходимо отметить ряд точек А, В, С, D, E, S. Начальный участок диаграммы ОА прямая наклонная линия. Напряжения σ в образце прямо пропорциональны деформации ε, т.е. соблюдается закон Гука: E. 12

12 Коэффициент пропорциональности в законе Гука Е называется модулем упругости материала. Точке А соответствует напряжение П предел пропорциональности. Пределом пропорциональности называется наибольшее напряжение, при котором деформация в материале прямо пропорциональна нагрузке: F П П A 0. Выше точки А диаграмма искривляется, закон Гука нарушается. Очень близко к точке А на криволинейном участке диаграммы можно отметить точку В, соответствующую пределу упругости У Пределом упругости называется наибольшее напряжение, при котором в материале возникает только упругая деформация: У Начиная от точки С диаграмма имеет горизонтальный (или почти горизонтальный) участок, которому соответствует предел текучести T. На этом участке деформации растут без увеличения нагрузки материал как бы течет. Пределом текучести называется напряжение, при котором деформация возрастает без заметного увеличения нагрузки: F У A 0 F Т Т A 0.. Горизонтальный участок диаграммы CD называют площадкой текучести, возникновение которой связано с явлением текучести. Площадка текучести ярко выражена только для малоуглеродистых сталей. Точке Е диаграммы соответствует напряжение B предел прочности. Пределом прочности называется наибольшее напряжение, которое выдерживает материал, не разрушаясь: F В В A 0. 13

13 До достижения предела прочности продольные и поперечные деформации образца равномерно распределяются по его длине. После достижения точки Е диаграммы эти деформации концентрируются в одном наиболее слабом месте, где начинается образовываться шейка местное значительное сужение образца (рис. 9). l 0 d ш l p Рис. 9. Образец до и после испытания. С этого момента продольная деформация зависит уже не столько от длины образца, сколько от его диаметра. За точкой Е нагрузка падает, что объясняется уменьшением поперечного сечения шейки, и происходит разрыв образца. Этому на диаграмме соответствует точка S и напряжение P. FР Истинное сопротивление разрыву Р. Aш Если начиная с некоторой точки К диаграммы (рис. 10) разгружать образец, то диаграмма будет представлена прямой КК 1, параллельной прямой ОА. Отрезок ОК 1 равен остаточной деформации 0, соответствующей напряжению, представленному ординатой точки К, а отрезок К 1 К 2 упругой деформации, при том же напряжении. Полная y деформация ε равна сумме указанных деформаций y 0. Если вновь начать нагружать образец, то диаграмма образует небольшую петлю. Эта петля, заштрихованная на рис. 10, получается за счет необратимых потерь энергии деформации. Она носит название петли гистерезиса. Начиная с точки К линия диаграммы пойдет так, как будто не было разгрузки и повторной нагрузки. Это показывает, что при нагружении образца выше предела текучести и последующей 14

14 его разгрузке материал образца изменил свои свойства: пропала площадка текучести, повысился предел пропорциональности и уменьшилась полная деформация при разрыве ( K1S2 OS2 ). σ E L K S σ’ п σ п А О K 1 K 2 ε 0 ε y S 2 Рис. 10. Диаграмма растяжения с петлей гистерезиса ε Такое изменение свойств металла носит название наклепа. Наклеп может возникнуть не только при растяжении, но и при любых других видах деформации. Иногда наклеп используют в технике. Например, цепи грузоподъемных машин предварительно вытягивают для возникновения в них наклепа, с целью уменьшить деформацию и повысить предел пропорциональности. При повторной разгрузке образца, начиная с некоторой точки L, произойдет повторение описанного явления наклепа. Высокоуглеродистые стали и некоторые другие материалы, не имеют площадки текучести. Предел текучести для этих материалов принимается условно равным напряжению, при котором остаточная деформация образца составляет 0,2%. Эта величина называется условным пределом текучести и обозначается σ 0,2. Прочностными характеристиками, определяемыми при растяжении являются: предел пропорциональности П, предел упругости У, предел текучести Т, предел прочности В и истинное сопротивление разрыву Р. 15

15 Пластичность характеризуется относительным остаточным удлинением при разрыве и относительным остаточным поперечным сужением при разрыве. Для определения характеристик пластичности изменяют диаметр шейки d ш и длину образца l P после разрушения. Используя эти величины, вычисляют l l l 2 P P 0, Aш d ш / 4. Относительное остаточное удлинение при разрыве определяется по формуле l р 100%. l 0 Относительное остаточное поперечное сужение равно A0 Aш 100%, A0 где A ш площадь поперечного сечения шейки. По величинам δ и ψ материалы условно делятся на пластичные и хрупкие. Материал считается пластичным, если относительная остаточная деформация больше 5%. Для стали марки Ст3 относительная остаточная деформация δ 21%, у высокопрочных сталей эта величина снижается до 7 10%. Величина δ зависит от соотношения длины образца и его поперечных размеров. Относительное остаточное сужение ψ более точно характеризует пластичность материала, поскольку оно в меньшей степени зависит от формы образца. Для стали Ст3 ψ составляет 50 60%. Порядок проведения работы. Испытанию подвергаются несколько образцов из различных металлов. Обмеренные образцы последовательно устанавливаются в захваты машины и подвергаются деформированию. В процессе испытания ведется наблюдение за поведением образца, получается диаграмма растяжения. После разрушения образца замеряются необходимые для расчетов величины l Р, d ш и производятся необходимые вычисления. 16

16 Протокол испытания Образцы до и после испытания Таблица 2.1 l о, мм d о, мм A о, мм 2 Эскизы образца Размеры образцов до испытания Образец 1 Образец 2 Образец 3 Результаты испытания образцов F кн Диаграммы растяжения образцов l м 17

17 Таблица 2.2 Усилия и деформации образцов при испытании F П F У F Т F В Δl р d ш Образец 1 Образец 2 Образец 3 Обработка результатов испытаний Таблица 2.3 Характеристики материалов Образец 1 Образец 2 Образец 3 σ П σ У σ Т σ В δ ψ Контрольные вопросы 1. Назовите и охарактеризуйте зоны диаграммы растяжения пластичной стали. 2. Дайте определение упругих и пластичных деформаций. 3. Что относится к механическим характеристикам материала? 18

18 4. Назовите прочностные характеристики материала. Как они определяются? 5. Какие величины относятся к характеристикам пластичности? 6. Упругие деформации. Пластические деформации, определения. 7. Опишите явление наклепа. Лабораторная работа 3 ИСПЫТАНИЕ МАТЕРИАЛОВ НА СЖАТИЕ Цель работы: Изучение поведения пластичных и хрупких материалов, испытание дерева при сжатии и определение их прочностных характеристик. Образцы для испытаний. Испытаниям подвергаются образцы из дюралюминия или мягкой стали (пластичный материал) и чугуна (хрупкий материал), дерева. Металлические образцы изготавливаются в виде круглых цилиндров (h 2d), деревянные в Рис. 11 Образцы для испытания на сжатие форме кубиков (рис. 11). Испытательная машина. Испытания проводятся на стенде. Содержание работы. Различные материалы имеют различные механические характеристики, в соответствии с которыми они разделяются на пластичные и хрупкие. Пластичные материалы при нагружении способны образовывать большие остаточные (пластические) деформации. К пластичным материалам, например, относятся медь, алюминий, латунь, малоуглеродистая сталь. Мерой пластичности является относительное остаточное удлинение при разрыве δ. Чем больше δ, тем более пластичным считается материал. Хрупкие материалы разрушаются без образования заметных остаточных деформаций. К хрупким материалам относятся чугун, высокоуглеродистая инструментальная сталь, стекло, кирпич, строительные камни. Для таких материалов величина удлинения δ при разрыве не превышает 2 5%, а в ряде случаев измеряется долями процента. 19

19 При испытании пластичных материалов на сжатие получается график зависимости между сжимающей силой и длиной образца диаграмма сжатия. На рис. 12 представлена диаграмма сжатия и растяжения пластичной стали для величин σ, ε. Начальный участок ОА этих графиков прямая линия. Точке А соответствует предел пропорциональности материала П, который незначительно отличается от предела текучести. Как видно из рис. 12, пределы пропорциональности и текучести при растяжении и сжатии для пластичных материалов одинаковы. Можно заметить, что при сжатии нет ярко выраженной площадки текучести. сжат. Т А раст. Рис. 12. Диаграммы испытаний пластичной стали Рис. 13 Пластичный образец до и после испытания Объясняется это тем, что при сжатии за пределом текучести растут пластические деформации, происходит быстрое увеличение величины поперечного сечения, следовательно, и жесткости образца. Образец принимает бочкообразную форму (за счет трения на торцах, стесняющего поперечную деформацию концов образца) и может быть сплющен в диск (рис. 13). Разрушить образец не удается, поэтому определение предела прочности при сжатии для пластичного материала лишено смысла. 20

20 Прочностная характеристика пластичного материала при сжатии — это предел текучести (предел пропорциональности) F Т Т A 0. Диаграмма сжатия хрупкого материала представляет почти прямую, слегка выпуклую линию вплоть до разрушения. На рис. 14 диаграмма сжатия приведена вместе с диаграммой растяжения. Разрушение происходит внезапно. Чугунный образец принимает слегка бочкообразную форму, что свидетельствует о наличии небольших пластических деформаций. На поверхности образца появляются продольные и наклонные трещины, что свидетельствует о слабом сопротивлении чугуна растягивающей деформации (рис. 15). σ В с сжат. σ В р раст. δ Рис. 14. Диаграммы испытаний хрупкого материала Единственной характеристикой для хрупкого материала при сжатии, которую можно определить из опыта, является предел прочности F В B A 0. Рис. 15 Хрупкие образцы после испытания Сопоставление предела прочности хрупких материалов при растяжении B р с пределом прочности при сжатии Bc показывает, что 21

21 для этих материалов k B p Bc (см. табл. 3.1). Величина отношения B р Bc — для чугуна колеблется в пределах 0,2 0,4, а для керамических материалов — k = 0,1 0,2. Таблица 3.1. Характеристики прочности и пластичности для некоторых конструкционных материалов Материал Предел текучести, МПа, при растяжении сжатии Предел прочности, МПа, при растяжении сжатии Относительное удлинение, % Сталь малоуглерод Сталь 30 незак Сталь 30 зак Сталь 45 незак Сталь 45 зак Сталь ЗОХГСА зак Сталь 40ХНВ зак Чугун серый СЧ ,6 Медь отожженная Медь прутковая Дюралюминий Текстолит ,5 Резина 0,04 18 Сосна вдоль волок Кирпич 0,3-0,07 3,0-0,7 Бетон 8,0-1,0 17,0-8,5 Имеет свои особенности испытание образцов из дерева. Дерево по своим свойствам существенно отличается от других конструкционных материалов тем, что оно обладает анизотропией прочностных и упругих свойств. Диаграмма сжатия дерева может иметь сложный вид, но в основном, при действии нагрузки поперек волокон она имеет вид, близкий к диаграмме сжатия пластичных материалов. При сжатии дерева вдоль волокон диаграмма получается как для хрупких материалов. В зависимости от соотношения прочностей вдоль и поперек воло- 22

22 кон, разрушение может происходить либо в виде расслоения вдоль волокон, либо в результате скола по наклонной линии к продольному направлению. Порядок проведения работы. При испытании пластичного материала нагружение нужно прекратить после того, как образец сожмется от первоначальной высоты на одну треть. После испытаний образцы следует сохранить и зарисовать. Определив значения характерных нагрузок F В, F Т, нужно затем вычислить прочностные характеристики. Протокол испытания Образцы дои после испытания Эскиз образца Таблица 3.2 l о, мм d о, мм A о, мм 2 Размеры образцов до испытания Образец 1 Образец 2 Образец 3 Таблица 3.3 Усилия и деформации образцов при испытании F П F У F Т F В Образец 1 Образец 2 Образец 3 23

23 Результаты испытания образцов F кн l Диаграммы сжатия образцов Обработка результатов испытаний Таблица 3.4 Характеристики материалов Образец 1 Образец 2 Образец 3 σ П σ У σ Т σ В 24

24 Контрольные вопросы 1. Какие материалы называются пластичными, хрупкими? 2. Какие механические характеристики определяются для пластичного материала при сжатии? Для хрупкого материала? 3. Опишите диаграмму сжатия пластичных и хрупких материалов. 4. Опишите картину деформирования и разрушения различных материалов при сжатии. Лабораторная работа 4 ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК УПРУГОСТИ МАТЕРИАЛА Цель работы: определение модуля упругости Е, коэффициента Пуассона ν и модуля сдвига материала G; опытная проверка закона Гука при растяжении. Образцы для испытаний стержни прямоугольного поперечного сечения шириной b и толщиной h. Испытательная машина. Исходя из условий ступенчатого нагружения и наибольшей максимальной нагрузки, принимается механическая машина SZ-10-1 или МР-05. Измерительные приборы. На образце устанавливаются два рычажных тензометра Гуггенбергера с базой l = 20 мм и коэффициентом увеличения Т 2 k = один в продольном, другой в поперечном направлении (рис. 16). Содержание работы. Диаграммы растяжения Т 1 или сжатия для большинства материалов на начальном участке прямолинейны. Эта закономерность является законом Гука: нормальное напряжение в поперечном сечении прямо пропорцио- h нально деформации: b Рис.16. Схема установки тензометров Е, где Е модуль упругости, величина постоянная для каждого материала. 25

25 Закон Гука может быть записан также в виде Nl l. EA Из последней формулы видно, что стержень деформируется тем меньше, чем больше модуль упругости материала. Таким образом, модуль упругости коэффициент пропорциональности в законе Гука, является мерой жесткости материала. Выразив E из закона Гука, получим формулу, которой можно воспользоваться для экспериментального определения модуля упругости: Nl E. la Известно, что продольная и поперечная ‘ деформации при растяжении связаны между собой зависимостью: ‘, где — коэффициент Пуассона (коэффициент поперечной деформации), характеризующий способность материала деформироваться в поперечном направлении при действии продольной силы. Величина постоянна для каждого материала и может принимать значения в пределах По определению коэффициент Пуассона численно равен отношению поперечной деформации к продольной, взятому по абсолютной величине: ‘. Модуль упругости Е и коэффициент Пуассона определяют свойства упругости материала. В табл.4.1 приведены величины Е и для некоторых конструкционных материалов. Модуль сдвига G можно выразить через E и : E G. 2(1 ) Как видно из приведенных зависимостей, для экспериментального определения модуля упругости и коэффициента Пуассона надо растя- 26

26 нуть или сжать образец, измерить усилие и деформации (продольную и поперечную), а затем произвести вычисления. Таблица 4.1. Модули упругости и коэффициенты Пуассона некоторых материалов Материал Модуль продольной упругости,10 5 МПа Коэффициент Пуассона Сталь углеродистая 2,0-2,1 0,24-0,30 Алюминиевые сплавы 0,72 0,33 Магниевые сплавы 0,40-0,47 0,34 Медь 1,0-1,3 0,31-0,34 Чугун 1,15-1,6 0,23-0,27 Дерево 0,1-0,12 Бетон 0,15-0,23 0,16-0,18 Резина 0,00008

0 Порядок выполнения работы. На образце вставленного в захваты испытательной машины устанавливаются тензометры Т 1 и Т 2 (рис.15). Нагружение проводится с помощью ручного привода ступенями F кгс. Всего берется 4-5 ступеней (при наибольшей нагрузке, напряжение в образце не должно достигать предела пропорциональности). На каждой ступени нагрузки снимаются показания тензометров и результаты измерений заносятся в табл.4.2 Таблица 4.2 Резльтаты показаний тензометров F, кгс F, кгс Т 1, мм Т 1, мм Т 2, мм Т 2, мм Показания тензометров на первой ступени принимаются за нуль отсчета, определяются средние приращения Т 1ср и Т 2ср, приходящиеся на одну ступень нагрузки. По результатам измерений находятся модуль упругости, коэффициент Пуассона: 27

27 Flk T2 cp E. T A T 1cp 1cp а затем вычисляется модуль сдвига E G. 2(1 ) Справедливость закона Гука проверяется построениями графика «деформация нагрузка» (Т-F), при этом значение силы и показание тензометра Т 1 на первой ступени отбрасываются и принимаются за начало координат. Если график является прямой линией, закон Гука считается подтвержденным. Протокол испытания Измерительные приборы:. ; l = мм ; k =.. Образец для испытания: Эскиз образца. h = мм, b = мм, A =. мм 2 28

28 Результаты испытаний: Таблица 4.1 Результаты испытаний образца F, кгс F, кгс Т 1, мм Т 1, мм Т 2, мм Т 2, мм Т 1 ср. Т 2 ср. Е =.. МПа; =..; G =.. МПа. F Диаграмма растяжения Т 29

29 Контрольные вопросы 1. Сформулируйте закон Гука. 2. Что такое модуль упругости? Какое свойство материала он характеризует? 3. Дайте определение коэффициента Пуассона, что он характеризует? 4. Как опытным путем определяются Е и ν? 5. Как экспериментально проверить закон Гука? Лабораторная работа 5 ИСПЫТАНИЕ МАТЕРИАЛОВ ПРИ КРУЧЕНИИ Цель работы: изучение поведения пластичных и хрупких материалов и дерева при кручении и определение их прочностных характеристик. Образцы для испытаний. Испытаниям подвергаются образцы круглого сечения из мягкой стали (пластичный материал) и алебастра или гипса (хрупкий материал), дерева. Перед испытанием измеряется диаметр образца и на его боковую поверхность наносится черта вдоль образующей. Испытательная машина Универсальный стенд МИ-40 для испытаний на кручение. Содержание работы. При кручении стержня круглого сечения материал находится в условиях плоского напряженного состояния. По площадкам, принадлежащим поперечным и диаметральным сечениям, действуют только касательные напряжения (рис. 17), т.е. имеет место чистый сдвиг. Главные напряжения действуют по площадкам, наклоненным к оси под углом Характер разрушения материала в таких условиях зависит от соотношения сопротивления сдвигу и отрыву. Разрушение пластичных материалов, для которых сопротивление сдвигу меньше, чем отрыву, происходит незаметно и бесшумно по сечению, перпендикулярному к оси (рис. 18а). Сечение в месте разрушения гладкое и отполированное; продольная черта, нанесенная на боковую поверхность образца, обращается в винтовую линию, что свидетельствует об образовании пластических деформаций. 30

30 3 1 а) 1 3 б) Рис.16. Схема нагружения и характер разрушения различных материалов Образцы хрупких материалов, для которых сопротивление срезу больше, чем отрыву, разрушаются с шумом и по винтовой поверхности, наклоненной к оси примерно на 45 0 (рис. 18б). Продольная черта почти не искривляется, т.е. пластические деформации отсутствуют. У деревянных стержней первые трещины возникают по образующим цилиндра, так как древесина плохо сопротивляется действию касательных напряжений, направленных вдоль волокон (рис. 18в). Диаграммы кручения показаны на рис. 19. На диаграммах М к — крутящий момент, — угол закручивания. Поскольку разрушение происходит без образования шейки, диаграмма пластичного материала (рис. 19а) не имеет нисходящего участка; диаграмма для хрупкого материала внешне похожа на диаграмму сжатия (рис. 19б). Для пластичного материала по концу прямолинейного участка диаграммы находится предел пропорциональности Рис. 19. Диаграммы кручения пластичного и хрупкого материалов в) Рис

31 М П П, Wp 3 d где W p — полярный момент сопротивления. 16 Предел прочности при кручении для пластичного материала можно вычислить по приближенной формуле 3 М В В. 4 W Для хрупкого материала диаграмма мало отличается от прямой, поэтому предел прочности можно вычислить по формуле M В В. W Порядок проведения работы. Образец устанавливается в захватах, при этом надо обратить внимание на его центрирование. Настраивается диаграммный аппарат, и образец медленно и плавно нагружается до разрушения. После разрушения по контрольной стрелке отмечается значение максимального момента. Определяются масштабы по осям М к и. Находят значение М п для пластичного материала, а затем значение п. Для хрупкого и пластичного материала определяются значения в по приведенным формулам. Протокол испытания Испытательная машина. ; Образцы для испытания: p p Сталь l 0 Ст = мм, d 0 Ст = мм, Эскиз образца. W p = мм 3. 32

32 Алебастр l 0 а = мм, d 0 а = мм, Эскиз образца. W p = мм 3. Дерево l 0 д = мм, d 0 д = мм, Эскиз образца. W p = мм 3. М Результаты испытаний: М М Машинные диаграммы М max м =. кгм, М max а =. кгм, М max д = кгм. 33

33 Обработка результатов: Масштаб по оси ординат: m М = ; М П м = кгм; Медь Характеристики прочности: П м = МПа; Алебастр В а = МПа; Дерево В д = МПа; Контрольные вопросы. 1. Охарактеризуйте напряженное состояние материала при кручении бруса круглого сечения. 2. Как происходит разрушение при кручении образцов пластичного и хрупкого материалов, дерева? 3. Какой вид имеют диаграммы кручения? 4. Как определяются механические характеристики материалов при кручении? 5. Сравните значение П и В с пределами пропорциональности (текучести) и прочности при растяжении. 34

34 Лабораторная работа 6 ОПРЕДЕЛЕНИЕ ПРОГИБОВ КОНСОЛЬНОЙ БАЛКИ ПРИ КОСОМ ИЗГИБЕ Цель работы — определить опытным путем прогиб свободного конца консольной балки и сравнить полученные данные с результатами теоретического расчета. Образцы для испытаний. Испытаниям подвергаются два образца, представляющих собой стержни длиной l, с поперечным сечением в виде прямоугольника с размерами b h и квадрата — a a. Испытательная установка. Образец 1 защемляется одним концом в корпусе 2 установки (рис.20) так, чтобы главная ось поперечного сечения у составляла заданный угол с вертикальной плоскостью. К свободному концу образца прикладывается сила F (груз 3). Для измерения прогиба конца балки используют миллиметровую бумагу, прикрепленную к пружинящему экрану 4. С помощью лимба 5 балка устанавливается с нужным углом наклона. φ x υ x υ υ y y γ Рис. 20. Схема испытательной установки Содержание работы. Изгибом называется такой вид нагружения стержня, при котором в его поперечных сечениях действует изгибающий момент. При плоском изгибе плоскость действия изгибающего момента проходит через главную ось поперечного сечения стержня. 35

35 F y Косым изгибом называется такой вид нагружения, при котором плоскость действия изгибающего момента не проходит через главную ось поперечного сечения стержня. Если главная ось у балки прямоугольного поперечного сечения b h наклонена на угол к вертикали, то при действии вертикальной нагрузки будет иметь место косой изгиб. При выполнении работы необходимо определить величину полного прогиба балки u и угол, который определяет линию прогиба. Раскладывая приложенную к образцу силу F на две составляющих F x F sin, F cos, направленные по главным осям поперечного сечения х и у, получим, что от действия каждой из них возникает плоский изгиб стержня в соответствующей плоскости. При расчете на прочность используется условие: мах М W x x М W у y Fl cos Fl sin W W x y Используя результаты, полученные для плоского изгиба, прогибы свободного конца балки по направлениям осей х и у находим по формулам: 3 3 Fxl Fyl x, y, 3EJ 3EJ y 3 3 где J y hb 12 ; J x bh 12 — осевые моменты инерции поперечного сечения. Полный прогиб балки равен геометрической сумме его составляющих, : x у Fl x y cos J y sin J х. 3E Угол отклонения линии полного прогиба от оси y x J x arctg arctg tg. y J y Для балки квадратного поперечного сечения J J, поэтому при любом угле направление полного прогиба будет совпадать с направлением силы F. x x y. 36

36 Порядок проведения работы. Определить размеры испытуемых балок. Вычислить осевые моменты инерции и моменты сопротивления поперечного сечения. Исходя из условия прочности определить величину допускаемой нагрузки F для = 0 и = Образец прямоугольного сечения установить под углом = Острием на свободном конце образца проколоть миллиметровку. Полученная точка О (рис. 21) соответствует начальному положению центра тяжести поперечного сечения. Нагружая балку ступенями несколько раз (на каждой ступени нагрузка увеличивается на F), отметить на миллиметровке для каждой нагрузки положение центра тяжести поперечного сечения точки О 1, О 2, О 3 (рис. 21). Измерить величину полного прогиба ОО 3 и определить угол. Произвести теоретические расчеты и сравнить данные эксперимента с расчетными. Далее образец прямоугольного сечения установить так, чтобы = 0 и опыт повторить. Заменить образец прямоугольного сечения на образец квадратного сечения и повторить эксперимент при углах = 30 0 и = 0 0. x y Рис. 21. К измерению полного прогиба Протокол испытания Испытательная установка: Измерительные приборы. Образцы для испытания.. l =.мм. 37

37 Для сечения в виде прямоугольника: h =. мм, b =. мм, J x =. мм 4, J y =.. мм 4, W х =.. мм 3, W y =.. мм 3. Для сечения в виде квадрата: а = мм, J x = J y = мм 4, W x = W y = мм 3. Результаты испытаний: = ; F. F, кгс F, кгс υ, мм Угол отклонения прогиба =. Теоретические значения прогибов и угла отклонения: υ x = мм; υ у = мм ; υ = мм. =. T Э T Δ υ = 100% =.. % T Э T Δ = 100% = % 38

38 Контрольные вопросы: 1. Какой вид нагружения называется изгибом? 2. Какой вид нагружения называется плоским изгибом и косым изгибом? 3. Как определить величину и направление полного прогиба при изгибе? 4. Какие геометрические характеристики используются для определения прогиба балки? 5. В каких случаях углы и будут одинаковы? Лабораторная работа 7 ИЗМЕРЕНИЕ ДЕФОРМАЦИЙ ЭЛЕКТРОТЕНЗОМЕТРИЧЕСКИМ МЕТОДОМ Цель работы — определение коэффициента тензочувствительности тензорезисторов (тензодатчиков). Объект испытания — тензодатчики типа ПБ на бумажной подложке с базой 20 мм и омическим сопротивлением 200 Ом. Испытательная установка — тарировочная балка (рис.22) равного z l 0 l Рис. 22. Тарировочная балка сопротивления изгибу. Балка 1 жестко защемлена одним концом на основании 2. Тензодатчики приклеены на верхнюю поверхность тарировочной балки, компенсационный датчик приклеен к основанию установки. К основанию прикреплен кронштейн с резьбовым отверстием для нажимного винта 3, на штативе крепится индикатор часового типа 4 для измерения прогиба балки. 39

39 Измерительные приборы. Деформации измеряются с помощью тензодатчиков и цифрового тензометрического моста ЦТМ-5 с ценой 6 деления 5 ЕОД (единиц относительной деформации; 1 ЕОД = 10 ), прогиб балки замеряется индикатором часового типа. Содержание работы. Для измерения деформаций деталей машин и элементов конструкций часто используются датчики омического сопротивления. Изменение сопротивления наклеенного на деталь тензодатчика связано с деформацией этой детали соотношением R K T, (7.1) R где ε — измеряемая относительная деформация детали в направлении оси датчика; R, R омическое сопротивление датчика и изменение сопротивления датчика при деформировании, K T — коэффициент тензочувствительности. Таким образом, K T — это коэффициент пропорциональности между относительным изменением сопротивления датчика и измеряемой относительной деформацией детали в месте наклейки датчика. При использовании тензометрического моста ЦТМ-5 с ценой деления 5 ЕОД разница показаний прибора ΔT до и после деформирования детали зависит от изменения сопротивления датчика R при деформировании. Эта зависимость определяется формулой: R 6 2 T 10. (7.2) R С учетом соотношений (7.1), (7.2), получаем 2 6 K T T 10, (7.3) В данной работе, в качестве тарировочного устройства используется балка равного сопротивления изгибу, у которой высота сечения h постоянна по всей длине, а ширина изменяется по линейному закону (рис. 23). Отметим, что балкой равного сопротивления изгибу называется балка, у которой, при изгибе, возникающие на верхних и нижних волокнах максимальные нормальные напряжения одинаковы по всей длине. 40

40 Как видно из формулы (7.3), при определении коэффициента тензочувствительности K T используются значения линейной деформации ε и изменение показаний прибора ΔT до и после деформирования детали. В данной работе величина ΔT будет определятся экспериментально, а величина ε — теоретически. Для нахождения ΔT используются тензодатчики, наклеенные на F l верхнюю поверхность балки и соединенные с ЦТМ-5. h Использование тарировочного устройства в виде балки равного сопротивления изгибу обу- у z l 0 словлено тем, что значению прогиба балки на некотором расстоянии от свободного конца b Рис. 23. Схема балки равного сопротивления вид сверху соответствует определенная величина относительной деформации ε волокна балки в месте наклейки датчика. Следовательно, замеряя прогиб балки, можно определять величину деформации. Найдем зависимость между прогибом балки равного сопротивления и величиной относительной деформации. Высота сечения балки h постоянна по всей длине, а ширина изменяется по линейному закону (рис.22). z b z, (7.4) где — коэффициент, зависящий от длины и наибольшей ширины балки ( b l / l ). Максимальное значение нормального напряжения в произвольном поперечном сечении балки определяется по формуле z z M z 6Fz 6F zh zh h M 6. (7.5) W b 41

41 Получается, что напряжения в крайних волокнах балки постоянны по всей ее длине, поэтому она и называется балкой равного сопротивления изгибу. По закону Гука относительная деформация крайних волокон 6F. (7.6) 2 E E h Как видно из последней формулы, деформация в крайних волокнах также постоянна по всей длине балки. Определим величину прогиба в сечении z. Дифференциальное уравнение изогнутой оси балки имеет вид: Следовательно, EJ 2 d 2 dz z M z Fz. 2 d 2 dz Fz EJ 12Fz 12F 3 3 z Ebzh Eh Интегрируя дважды это уравнение и используя граничные условия d (балка защемлена на правом конце: l 0; l 0 ), получим dt 2 ( z) 6F l z E h. Из последнего равенства следует, что 3 F E h ( z) l z. Подставив это выражение в формулу (7.6), получим F 6E h ( z) h ( z). (7.7) 3 2 E h l z h E l z Если прогиб балки в сечении z = l l 0 равен 0, то в соответствии с (7.7) деформация крайних волокон 2 0. h 0. (7.8) l 42

42 В формулу (7.8) не входят ни характеристики упругих свойств материала балки, ни коэффициент. Множитель перед 0 постоянная величина. Подставляя выражение (7.8) в равенство (7.3), получим формулу для определения коэффициента тензочувствительности: 5 2 T 10 l0 K T. (7.9) h0 5 Поскольку деформация крайних волокон балки равного сопротивления постоянна по всей длине, то тензодатчики можно наклеивать в любом месте на верхней или нижней поверхности балки. Порядок проведения работы. На тарировочную балку с наклеенными тензорезисторами, устанавливается индикатор. Тензорезисторы с помощью штекерного разъема подключаются к прибору ЦТМ-5. Измеряются толщина балки h и расстояние l 0. С помощью нажимного винта балке задается небольшой начальный прогиб υ, стрелка индикатора устанавливается на нуль. Переключателем прибора производится поочередное подключение всех датчиков к измерительному мосту ЦТМ-5 и снимаются начальные показания Т i (i = 1 N, где i — номер тензорезистора, N число датчиков). Затем, с помощью нажимного винта производится нагружение балки, задается другая величина прогиба υ и снимаются показания Т i прибора. Для получения более точных результатов производят 2-3 нагружения, на каждом из которых задается одинаковое приращение прогиба Δυ = υ 0. Показания прибора снимаются для 4-5 датчиков. Результаты измерений заносятся в таблицу. Затем для каждого датчика подсчитываются величины ΔT i изменения показаний прибора. Коэффициент тензочувствительности тензорезисторов вычисляется по формуле, аналогичной (7.9): T cp 0 T, h 5 где ΔT ср — среднее изменение показаний прибора. K 0 l 43

43 При подсчете ΔT ср вначале находят среднюю величину ΔT i ср для каждого датчика с номером i, а затем среднюю величину ΔT для всех датчиков. Используются формулы: m Tj Ti cp j i Ti cp ; T cp, m N где m число ступеней нагружения, N число датчиков. Протокол испытания Испытательная установка. Измерительные приборы. Образцы для испытания: h =.. мм; N l 0 =..мм. Результаты испытаний: m υ, мм υ 0, мм Показания ЦТМ Датчик 1 Датчик 2 Датчик 3 Датчик 4 Т 1 ΔТ 1 Т 2 ΔТ 2 Т 3 ΔТ 3 Т 4 ΔТ 4 ΔT i ср ΔT ср = Коэффициент тензочувствительности К Т = 44

44 Контрольные вопросы: 1. Как устроен тензорезистор и на чем основан принцип измерения деформаций с его помощью? 2. Как измеряется омическое сопротивление с помощью электрического измерительного моста? 3. С какой целью в цепь измерительного моста включается компенсационный датчик? 4. Что такое коэффициент тензочувствительности тензорезистора? 5. Что такое балка равного сопротивления? Как связаны между собой ее прогиб и деформация крайних волокон? 6. Опишите устройство и работу тарировочной балки. 7. С какой целью при экспериментальном исследовании нагружение образца осуществляется ступенями? 8. Почему величину ΔT осредняют для различных ступеней нагружения и для разных датчиков? Лабораторная работа 8 ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ ПРИ ВНЕЦЕНТРЕННОМ РАСТЯЖЕНИИ Цель работы экспериментально определить нормальные напряжения в крайних точках поперечного сечения стержня при внецентренном растяжении и сравнить полученные результаты с расчетными данными. Испытание проводится на механической машине SZ 10-1, шкала 1000 кг. Измерительные приборы. Используются тензодатчики или механические рычажные тензометры Гуггенбергера с базой l = 20 мм и коэффициентом увеличения k = Опыт проводится на машине SZ 10-1, со шкалой до 1000 кг. Содержание работы. Внецентренным растяжением называется такой вид нагружения стержня, при котором внешняя продольная сила действуют по линии, параллельной оси стержня (рис. 24). Определение напряжений в этом случае производится с использованием принципа независимости действия сил. Если привести внешнюю продольную силу к центру тяжести поперечного сечения стержня, то получится, что в поперечном сечении действуют продольная 45

45 y сила N F и изгибающие моменты M x F yf, M y F xf, где x F, y F — координаты точки приложения силы F (рис. 24). Следовательно, в общем случае, внецентренное растяжение-сжатие представляет собой сочетание осевого растяжения и косого изгиба. При этом, продольная сила N F и изгибающие моменты M x, M y вызывают возникновение в поперечных сечениях нормальных напряжений z F F N A M y M x y у J J х M, (8.1) x y y F A где A, J x, J — площадь и осевые мо- x менты инерции поперечного сечения стержня. y, x — координаты точек сечения. B Суммируя нормальные напряжения (8.1), получим, что при внецентренном растяжении в сечениях напряжений Рис. 24. К определению стержня действуют напряжения F M M x y у х. (8.2) A J J Схема используемого в лабораторной работе образца представлена на рис.25. В данном случае поперечное сечение стержня квадрат с длиной стороны a. Продольная сила действует по оси, проходящей через точку, расположенную на оси оx, с координатами x F a, y F 0. Следовательно, M 0, M y Fa, x x y 2 4 A a, a 12 J y (8.3) и формула (8.2) принимает вид: F M y х. (8.4) A J y x F 46

46 С учетом (8.4) получатся, что напряжения в крайних точках сечения (точки В и А), при х a 2 вычисляются по формулам: F M y F M B, y A, (8.5) A Wy A Wy 3 где W 2J a a 6 момент сопротивления сечения. Условие прочности имеет вид: F F F M y F Pa мах. (8.6) A Wy A W Рис. 25. Схема установки y Из (8.6) получается следующая формула для определения допускаемой величину силы F: 1 a F ( ). (8.7) A Для экспериментального определения напряжений с помощью тензометров нужно найти деформации крайних волокон сечения, затем с использованием закона Гука E, вычислить напряжения в этих волокнах. Порядок проведения работы. Измеряются размеры поперечного сечения стержня и вычисляются его геометрические характеристики A,. Находится допускаемая величина силы F. W у F F При экспериментальном определении напряжений тензометры устанавливаются на сторонах образца, на которых находятся точки А и В (рис. 24). В дальнейшем величины, относящиеся к указанным сторонам, будут отмечаться, соответственно, индексами А и В). Производится пошаговое нагружение образца, при этом величина приращения нагрузки F выбирается с таким расчетом, чтобы сделать 3 4 нагружения. На каждом шаге нагружения снимаются показания тензометров Т А i, Т В i (i номер тензометра) и данные заносятся в таблицу. Затем подсчитываются средние приращения показаний тензометров y W y y 47