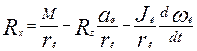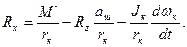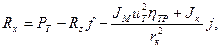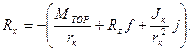Нормальная и касательная реакция дороги, действующие на колесо (ведомое, ведущее, тормозное)

При движении подвижного состава его колеса могут катиться в различных режимах: тяговом ведомом и тормозном. При этих режимах качения со стороны дороги на колеса действуют различные реакции. Для определения их велечины рассмотрим качение колеса подвижного состава по жесткой дороге.

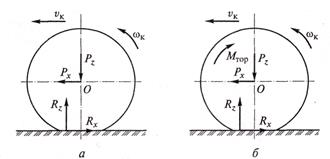
Силы Р_х и Р_z и момент М действуют на колесо со стороны подвижного состава. Силы R_х и R_z действуют на колесо со стороны дороги и представляют собой реакции дороги.

Рассмотрим указанные силы и момент.

Р_z — вертикальная нагрузка на колесо, направлена вниз перпендикулярно поверхности дороги и представляют собой реакции дороги

Р_х – продольная сила, параллельна поверхности дороги. В зависимости от режима качения колеса может быть направлена как в сторону так и против движения подвижного состава

М – момент, подводимый к колесу полуосью или от тормозного барабана (диска). Иногда момент может быть равен нулю (не подводится к колесу). Момент считается положительным, если его направление совпадает с направлением вращения колеса, и наоборот

R_z — нормальная реакция дороги, направлена вверх перпендикулярно поверхности дороги. Точка приложения нормальной реакции смещена относительно оси колеса на некоторую велечину a_ш изза большой деформации шины в набегающей на дорогу части, чем в сбегающей с дороги части

R_х — касательная реакция дороги, расположена в плоскости дороги. В зависимости от режима качения колеса модет быть направлена в сторону, или против движения подвмжного состава. Касательная реакция считается положительной если она направлена по движению, и наоборот

Составим уравнение моментов относительно центра О колеса:

где J_к — момент инерции колеса относительно оси его вращения.

Из указанного выражения находим касательную реакцию дороги

Обозначим отношение а_ш/r_к через f и определив значение из выражения ускорения подвижного состава, получим выражение касательной реакции дороги в общем случае (для всех режимов качения колес)

Рассмотрим наиболее характерные режимы качения колеса

Тяговый режимхарактерен для ведущего колеса. Момент М подводится к колесу через полуось, и направление момента совпадает с направлением врощения колеса. Момент в этом случае называется крутящим. Подставим в выражение касательной реакции дороги вместо момента М значение момента М_к подводимого к ведущим колесам, и, учитывая значение ускорения j подвижного состава, для ведущего колеса получим

Для ведущего колеса касательная реакция R_x >0. Следовательно, она направлена в сторону движения.

Ведомый режимхарактерен для ведомого колеса. Момент М к колесу не подводитсяи следовательно он равен нулю. Для ведомого колеса касательная реакция дороги

знак минус говорит о том, что у ведомого колеса касательная реакция дороги направлена против движения

Тормозной режим характерен для тормозящего колеса (ведущего, ведомого). Момент М подводится к колесу от тормозного барабана или диска, и направление его противоположно направлению вращения колеса. Момент в этом случае называется тормозным. Подставив в выражение касательной реакции дороги вместо момента М значение тормозного момента (М=-М_тор) для тормозящего колеса, получим

знак минус говорит о том, что у тормозящего колеса касательная реакция дороги направлена против движения

Скорость и ускорение подвижного состава.

Линейную скорость колеса, м/с, можно определить с помощью выражения

где r_к — радиус колеса, м; ω_к— угловая скорость колеса, рад/с.

Скорость автомобиля при его прямолинейном движении равна линейной скорости колеса, т.е. v = vк.

Так как скорость автомобиля v обычно выражается в км/ч, а скорость колеса vк — в м/с, то для получения скорости автомобиля v в км/ч необходимо ввести переводной коэффициент 3,6. С учетом этого коэффициента скорость автомобиля, км/ч:

Аналогично при прямолинейном движении ускорение автомобиля равно линейному ускорению колеса:

(3.15)

Сила тяги и тяговая мощность на ведущих колесах

Реакции дороги, действующие при движении на колеса автомобиля

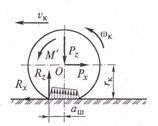
При движении автомобиля его колеса могут катиться в различных режимах: тяговом, ведомом и тормозном. При этих режимах качения со стороны дороги на колеса действуют силы, называемые реакциями. Для определения их величины рассмотрим качение колеса автомобиля по жесткой (недеформируемой) дороге. Схема сил, действующих в этом случае на ведущее колесо, представлена на рис. 3.5.

Силы Р_х и Р_z. и момент М’ действуют на колесо со стороны автомобиля. Силы R._x и R_z действуют на колесо со стороны дороги и представляют собой ее реакции.

Рассмотрим указанные силы и момент.

Рис. 3.5. Силы, действу­ющие на ведущее колесо при качении по недефор­мируемой дороге: О — центр колеса

Р_z. — вертикальная нагрузка на колесо, направленная вниз перпендикулярно поверхности дороги.

Р_х — продольная сила, параллельная поверхности дороги. В зависимости от режима качения колеса она может быть на­правлена как в сторону движения автомобиля, так и в противоположную.

M`— момент, подводимый к колесу от полуоси или тормозного барабана (тормозного диска). Иногда момент может быть равен нулю (не подводится к колeсу). Момент считается положительным, если его направление совпадает с направлением вращения колеса, и наоборот.

R_z — нормальная реакция дороги, направленная вверх перпенди­кулярно поверхности дороги. Точка приложения нормальной реак­ции смещена относительно оси колеса на некоторую величину а_ш из-за большей деформации шины в набегающей на дорогу части, чем в сбегающей с дороги. Это подтверждает эпюра элементарных сил, действующих в месте контакта колеса с дорогой, для кото­рых нормальная реакция является результирующей силой.

R_х — касательная реакция дороги. Это сила, которая действует в плоскости дороги и в зависимости от режима качения колеса может быть направлена в сторону движения автомобиля или в про­тивоположную. Касательная реакция считается положительной, если она направлена в сторону движения, и наоборот.

Составим уравнение моментов относительно оси колеса:

(3.16)

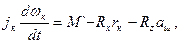
где J_к — момент инерции колеса относительно оси вращения. Из выражения (3.16) находим касательную реакцию дороги:

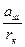
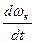
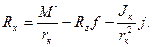
Обозначим отношение — символом ƒ и, выразив величину с помощью формулы (3.15) через ускорение автомобиля j,для касательной реакции дороги получим в общем случае (при любых режимах качения колеса)

(3.17)

Рассмотрим типичные режимы качения колеса.

Тяговый режим характерен для ведущего колеса. Момент М’ подводится к колесу через полуось, и направление момента со­впадает с направлением вращения колеса. В этом случае момент называется крутящим. Подставляя в выражение (3.17) вместо М’ выражение для крутящего момента М_к, подводимого к ведущим колесам, и учитывая соотношения (3.12) и (3.15), для ведущего колеса получим

Где 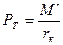— тяговая сила.

Для ведущего колеса касательная реакция R_х > 0. Следователь­но, она направлена в сторону движения, как показано на рис. 3.5.

Ведомый режим характерен для ведомого колеса. Момент М’ к колесу не подводится, и, следовательно, он равен нулю. Для ведомого колеса касательная реакция дороги

Знак «-» показывает, что у ведомого колеса касательная реакция дороги направлена Тормозной режим является характерным для тормозящего колеса(ведущего, ведомого). Момент М’ подводится к колесу от тормозного барабана или тормозного диска и направление его противоположно направлению вращения колеса. В этом случае момент называется тормозным (М_тор). Подставив в выражение (3.17) вместо М’ тормозной момент (М’ = -M_тор), для тормозящего колеса получи против движения (рис.3.6, а).

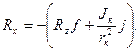
Рис. 3.6. Силы, действующие на ведомое (а )и тормозящее (б) колеса

при качении по недеформируемой дороге:

О — центр колеса

Знак «-» свидетельствует о том, что у тормозящего колеса касательная реакция дорога направлена против движения (рис. 3.6, б).

НОРМАЛЬНЫЕ РЕАКЦИИ ОПОРНОЙ ПОВЕРХНОСТИ, ДЕЙСВУЮЩИЕ НА КОЛЕСА ДВУХОСНОГО АВТОМОБИЛЯ

Нормальные реакции опорной поверхности, действующие на колеса автомобиля непрерывно изменяются в процессе движения. Эти реакции являются определяющими для сил сопротивления качению и сил сцепления с дорогой.

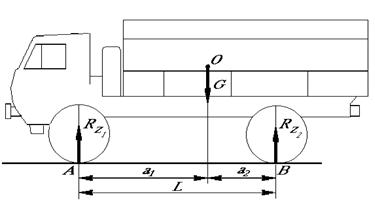
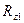
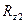
Рассмотрим вначале самый простой случай, определим нормальные реакции, действующие на колеса автомобиля, стоящего на горизонтальном участке дороги.(см. рис.2.5). Величины и можно определить, состав сумму моментов относительно точек контакта переднего (т.А) и заднего (т.В) колес.

В данном случае

(12)

(13)

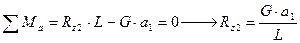
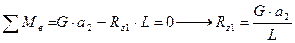
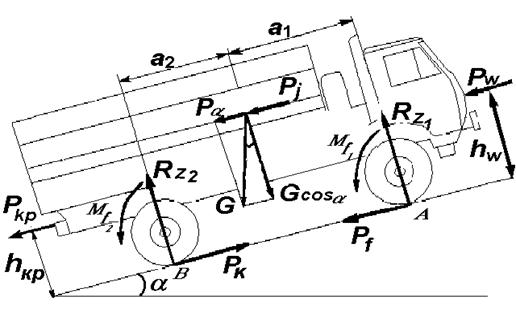
Далее рассмотрим более общий случай — автомобиль, движущийся с ускорением на подъем (рис.2. 6).

Составим уравнение равновесия относительно точек контакта передних и задних колес с опорной поверхностью

(14)

(15)

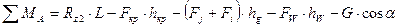
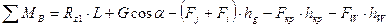
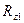
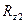
Из анализа этих уравнений видно, что при ускоренном движении на подъем реакции , будет меньше .

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Нормальные реакции опорной поверхности на колесах

Величины нормальных реакций на колесах ТС оказывают существенное влияние на силы сопротивления качению и сцепление с опорной поверхностью. Особое значение имеет характер перераспределения величин нормальных реакций на колесах при оценке поперечной устойчивости ТС, для формирования радиусов качения и соответственно изменения окружных сил на ведущих колесах. Распределение нормальных реакций по осям колес зависит как от конструктивных особенностей ТС, так и от условий его движения.

Учитывая, что транспортная машина при наличии подрессоривания является динамической колебательной системой, непрерывно изменяющей свое положение в пространстве, определение нормальных реакций на колесах ТС представляет собой довольно сложную задачу.

Однако при решении ряда конкретных задач возможно принять для анализа и определения вертикальных реакций на колесах ТС сравнительно простые модели. В частности, для определения величин нормальных реакций на колесах ТС принимается плоская расчетная модель. Движение ТС рассматривается при действии постоянных сил и моментов, траектория движения принимается неизменной, а характер

Рассмотрим наиболее простую схему ТС (см. рис.1) в виде автопоезда, состоящего из двухосного тягача и пассивного прицепного звена, движущегося по плоской поверхности. В случае полуприцепного варианта автопоезда несколько изменится схема действия сил: появляется дополнительно к тяговой силе в опорно-сцепном устройстве нормальная сила, обусловленная передачей части массы полуприцепа на тягач.

Из условия равновесия ТС получим

∑RZi = RZ1 + RZ2 = GТcosα. (1)

Для определения RZ2 приравняем к нулю сумму моментов, внешних сил и силы инерции относительно точки 1, считая положительными моменты, направленные против часовой стрелки

RZ2 = [(GТsinα + mJX)h + GТacosα + ∑Mfi + PWhW + PKPhKP]/L. (2)

Из уравнения (1) получим выражение для RZ1

RZ1 = [GТbcosα (GТsinα + mJX)h ∑Mfi PWhW PKPhKP]/L, (21)

где JX = dV/dt, a mJX – инерционная составляющая поступательного

движения ТС; m – масса ТС; α угол подъема дороги; GТ = mТg – сила тяжести тягача; h – высота расположения центра масс тягача от опор

ной поверхности; PW – сила сопротивления воздуха; hW – плечо приложения равнодействующей силы сопротивления воздуха к ТС; hKP – высота расположения сцепного устройства от поверхности дороги.

Рис. 2. Схема сил и моментов, действующих на многоосное ТС:

RZi – опорные реакции на колесах; Рfi, Mfi – соответственно сила и момент сопротивления качению; РКОi – окружная (тяговая) сила на колесе; РW – сила сопротивления воздуха; РКР – тяговое усилие в сцепном устройстве; V скорость движения; Ga – сила тяжести ТС; α угол подъема дороги

При неподвижном ТС, стоящем на горизонтальном участке дороги, нормальные реакции на колесах ТС будут равны:

а) для тягача: RZ1 = GTb/L; RZ2 = GTa/L; (аналогичные зависимости будут и для прицепа);

б) для полуприцепного звена: RZС= GП x/LC; RZ3 = GП(1 + x/LC),

где GП – сила тяжести прицепного звена; RZС – нормальная реакция в опорно-сцепном устройстве; х и LC – расстояние между осью колеса и центром масс и осью колеса и шкворнем полуприцепа (опорносцепным устройством) соответственно.

В случае многоосного ТС (рис.2) реакции опорной поверхности на колесах определяются также из условия равновесия сил, действующих на движущуюся машину [4].

∑RZi = RZ1 + RZ2 + …+ RZn = Gаcosα, (3)

Из уравнения моментов относительно точки 1 (передняя ось)

RZ1ℓ12 + RZ3ℓ13 +…+ RZnℓ1n = Gaℓ1cosα + (Gasinα + maJX)hg +

где ℓ1i – расстояние от первой оси до i-й; n – число осей.

При наличии тяговой связи с многоосным тягачом в уравнение (4)

добавляется выражение PKPhKP.

Следует отметить, что при наличии упругой связи колес с несущей рамой (корпусом) ТС [5] распределение нагрузки по осям будет различным, поэтому для определения реакций опорной поверхности

на колесах многоосной машины (см. рис.2) необходимо дополнительно составить уравнения изменения положения точек рамы ТС над соответствующими осями

RZi = СПРiZi (5) где СПРi = СРiСШi/(СРi + СШi) – приведеннaя жесткость системы подвеска-шина; СРi – жесткость i — й подвески, приведенная к колесу; СШi – жесткость шины i — го колеса, Zi перемещение точки рамы ТС, распoложенной над i — м колесом под действием нормальной реакции.

Выражая угол наклона рамы ТС под действием внешних сил ϕ, а перемещение i — го колеса через перемещение колеса первой оси Z1, формула для Zi будет

Zi = Z1 + ℓ1itgϕ (6)

Из формул (3), (5) и (6) получим

Z1 = (Gacosα ∑cПРiℓ1itgϕ)/∑СПРi . (7)

Решая совместно уравнения (4)…(7) и обозначая правую часть

уравнения (4) через А, определим tgϕ

tgϕ = (Gacosα∑СПРiℓ1i А∑СПPi)/[(∑СПРiℓ1i)2 ∑СПРiℓ1i2∑СПPi] (8)

Решая совместно уравнения (5)…(8), определим RZi:

RZi = СПPi(B + Eℓ1i), (9)

A∑СПРiℓ1i∑СПpi>/[∑СПPi(∑СПРiℓ1i)2 ∑СПРiℓ1i2(∑СПРi)2]; (10)

E = tgϕ = (Gacosα∑СПРiℓ1i А∑СПPi)/[(∑СПРiℓ1i)2 ∑СПРiℓ1i2∑СПРi (81)

Уравнение (9) справедливо для СТС, имеющего различную жесткость подвески колес и шин. Если допустить одинаковую величину жесткости подвески и шин всех колес и симметричное их расположение

по базе ТС, то уравнения (8) … (10) значительно упрощаются. Выведенные зависимости для определения реакций опорной поверхности на колесах справедливы и для СТС, представляющих собой сочлененные многозвенные автопоезда с опорно-тяговой связью.

Материал взят из книги Расчет тягово-скоростных свойств и топливной экономичности специальных транспортных средств (А.М. Петренко)