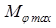Момент сопротивления качению колеса в ведомом режиме при прямолинейном движении

Во время прямолинейного движения эластичного колеса по твердой недеформируемой дороге подведенная к нему энергия расходуется на преодоления трений в резинокордовой оболочке, в резине протектора и в контакте колеса с опорной поверхностью. Эти три трения вызывают гистерезисные явления (потери) в шине.

Если колесо неподвижно, тогда нормальные реакции опорной поверхности симметричны относительно оси, проходящей через центр колеса, а следовательно их равнодействующая R_z проходит через центр колеса точку О (см. рис.3.2а )

Если приложить к колесу толкающую силу Р_тол, то при его движении из-за гистерезисных потерь в шине нормальные реакции опорной поверх-ности несимметричны. Эта несимметричность вызыва-ет смещение равнодейст-вующей нормальной реакции R_z по ходу движения на величину «а» (см. рис. 3.2.б).

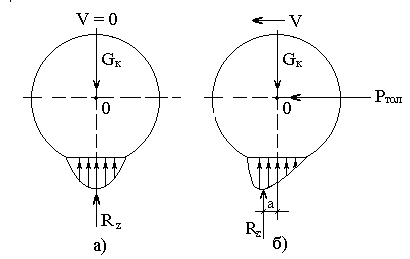
. Рис.3.2 Схема сил и реакций, действующих на колесо.

Смещение равнодействующей нормальных реакций относительно центра колеса вызывает момент, который определяется по формуле

Разделим правую и левую часть полученной зависимости на радиус колеса. Тогда имеем

.

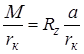
Безразмерную величину 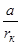назвали коэффициентом сопротивления качению и обозначили f. Частное от деления момента на радиус колеса назвали силой сопротивления качению и обозначили Р_f .

В этом случае имеем

,

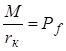
где Р_f – cила сопротивления качению в Н.

Окончательно сила сопротивления качению запишется

,

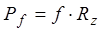
где R_z – нормальная реакция опорной поверхности в Н.

На горизонтальной дороге R _z = G _к ,

где G _к – нагрузка на колесо в Н.

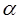
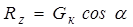
Если опорная поверхность имеет угол уклона , тогда равнодействующая нормальных реакций равна ,

а сила сопротивления качению Р_f запишется Р_f = .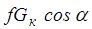

Момент сопротивления качению на дороге, имеющей уклон, равен

М_f= .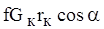

В полученной зависимости особый интерес представляет коэффициент сопротивления качению f, которыйзависит от целого ряда факторов. При этом основными из них являются:

— вид и состояние опорной поверхности. Минимальное значение коэффициент f имеет на асфальтобетонной сухой дороге. Его значение для тороидных шин и шин регулируемого давления при номинальном давлении воздуха находится в пределах 0,01…0,02;

— тип и конструктивные параметры шины. Минимальное значение коэффициент f на сухой асфальтобетонной дороге имеет для шин с металлокордом (f= 0,01) и максимальное (f=0,02) для шин с регулируемым давлением;

— скорость движения. С увеличением скорости движения из-за дополнительной деформации тела шины при ударах и колебательных процессах происходит увеличение затрат энергии на преодоление сопротивления качению шины. Увеличение коэффициента f, вызванное скоростью движения, учитывается эмпирической зависимостью

, (3.1)

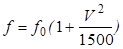
где V – скорость движения колеса в м/с;

f₀ – коэффициент сопротивления качению при скорости, равной нулю.

Кроме этих факторов, на величину коэффициента f влияют: степень износа протектора, температура шины, количество и материал слоев корда, качество применяемой резины, геометрические параметры шины, давление воздуха и др. Однако влияние этих факторов менее существенно по сравнение с выше

перечисленными и как правило их влиянием пренебрегают.

Момент сопротивления колеса автомобиля

Момент сопротивления повороту колеса автомобиля при движении

9.7.1 Mомент сопротивления повороту шины при движении

При повороте управляемого колеса на месте в контакте колеса с опорной поверхностью участвуют одни и те же элементы шины. Происходит вначале упругое закручивание тела шины между жестким ободом и элементами шины, контактирующими с опорной поверхностью. Если учесть, что практически для всех автомобилей центр поворота отпечатка (точка встречи оси шкворня с опорной поверхностью) находится в пределах отпечатка, то при повороте колеса на месте его перекатывание не будет, а угол закручивания тела шины равен углу поворота колеса.

При движении происходит постоянное обновление элементов шины, контактирующих с опорной поверхностью. Это обновление будет тем интенсивнее, чем больше скорость движения колеса и меньше размеры отпечатка шины. При повороте управляемого колеса во время движения, аналогично повороту колеса на месте, также происходит закручивание тела шины между жестким ободом и контактным отпечатком. Однако закручивание тела шины будет только в момент поворота колеса, который осуществляет через рулевое колесо водитель. Если водитель прекращает поворот колеса, то закручивание тела шины из-за обновления элементов шины с опорной поверхностью исчезает.

Что же касается скорости поворота управляемого колеса, то она зависит от скорости поворота рулевого колеса и передаточного числа рулевого управления. Очевидно, чем больше скорость поворота рулевого колеса, тем больше будет угол закручивания тела шины при постоянной скорости движения.

В общем случае элементарный угол закручивания тела шины при прохождении центром колеса элементарного пути ds равен

где — градиент закручивания тела шины, численно равный углу закручивания тела шины при прохождении колесом единицы пути;

ds -элементарный путь, на котором происходит закручивание тела шины.

Тогда величина угла закручивания запишется

В результате проведенных исследований [1], [2] было установлено, что при отсутствии угла продольного наклона шкворня закручивание тела шины управляемого колеса происходит при прохождении центром колеса пути а/2, где а- большая ось отпечатка шины. В результате чего имеем

Поскольку градиент закручивания тела шины не зависит от величины пройденного пути, вынесем его за знак интеграла. После решения интеграла получим

Разделив числитель и знаменатель на dt , получим

или окончательно имеем

где V — скорость движения центра колеса в м/с, поскольку ;

-угловая скорость поворота колеса в рад./с , поскольку .

При наличии продольного наклона шкворня формула (9.37) с учетом исследований запишется так

где r к — радиус колеса;

угол продольного наклона шкворня.

Заметим, что угловую скорость поворота управляемого колеса задает водитель поворотом рулевого колеса. При этом, как следует из анализа литературных источников, угловая скорость поворота рулевого колеса не превышает 1,5 об/с или 9,42 рад./с.

Скорость движения автомобиля изменяется в широких пределах от практически 1м/с до Vmax . Поскольку скорость находится в знаменателе выражения (9.38) и изменяется в широких пределах, поэтому она существенно влияет на величину угла закручивания тела шины. Очевидно, чем больше скорость движения автомобиля, тем меньше угол закручивания тела шины между жестким ободом и контактным отпечатком. А это подтверждает то обстоятельство, что при движении автомобиля, чем больше его скорость, тем меншее усилие прикладывает водитель при управлении автомобилем.

Анализ рассчитанных по формуле (9.38) данных показал, что при минимальных скоростях движения и максимальной скорости поворота рулевого колеса угол закручивания тела шины не превышает , т.е. находится на участке линейной зависимости момента сопротивления повороту шины на месте от угла поворота.

Учитывая, что угол поворота колеса на месте и угол закручивания тела шины при движении, рассчитанный по формуле (9.38), являются, с точки зрения явлений, определяющих сопротивление повороту шины, идентичными, вправе записать

где C — угловая жесткость шины относительно вертикальной оси;

M -момент сопротивления повороту шины при движении.

Заметим, что зависимость (9.39) получена при условии, что величина угла закручивания тела шины при движении находится на участке линейной зависимости момента сопротивления повороту шины от угла поворота.

Поскольку момент сопротивления повороту шины при движении будет иметь место только во время поворота управляемого колеса, поэтому его будем обозначать М , в то время как при повороте на месте обозначается M .

Момент сопротивления повороту шины на месте

Под моментом сопротивления повороту управляемого колеса понимается приведенный к оси шкворня момент, который необходимо приложить относительно оси шкворня, чтобы повернуть колесо.

Анализ конструктивных параметров управляемых мостов автомобилей показал, что центр поворота отпечатка, точка О, (точка встречи оси шкворня с опорной поверхностью см. рис.9.2) практически на всех автомобилях находится в пределах контактного отпечатка. В этом случае при повороте колеса на месте оно не будет вращаться относительно оси цапфы. Если же точка встречи оси шкворня с опорной поверхностью будет находиться за пределами контактного отпечатка, тогда при повороте управляемого колеса на месте оно будет вращаться относительно оси цапфы [1].

При повороте управляемого колеса на месте и при отсутствии его вращения относительно оси цапфы момент сопротивления его повороту М_к запишется

где М_j — момент сопротивления повороту шины на месте;

М_ст — весовой стабилизирующий момент;

М_тр— момент трения в подшипниках шкворневого узла;

Анализ составляющих в уравнении (9.2) показал, что момент М_j составляет 75-90% М_к; М_ст+М_тр— в сумме 10-25% М_к, а момент М_j®0. Поскольку М_j является определяющим в выражении (9.2), поэтому в литературных источниках часто приравнивают эти моменты между собой, считая М_к = М_j. В какой-то мере это объясняется затруднениями с определением весового стабилизирующего момента при комбинированном наклоне шкворня [1], [2].

Момент М_j в общем случае зависит от угла поворота колеса, формы и размеров контактного отпечатка, коэффициента сцепления, нагрузки на колесо, положения центра поворота отпечатка (точки встречи оси шкворня с опорной поверхностью) относительно геометрического центра отпечатка (см. рис.9.3).

Что же касается конкретно отпечатков шин, то они могут иметь форму овала, эллипса, приближаться к кругу, прямоугольнику. Для получения универсальных зависимостей, позволяющих определить момент М_j, отпечатки шин приводятся к равновеликим прямоугольникам. Для этого необходимо выполнить три условия:

1.Площади отпечатка и прямоугольника должны быть равны F₀ = F_пр,

где F₀, F_пр — площади соответственно отпечатка и приведенного прямоугольника.

2. Соотношения сторон прямоугольника и отпечатка равны между собой

,

где А,В — стороны отпечатка;

а,в — стороны равновеликого прямоугольника.

3. Геометрические центры прямоугольника и отпечатка должны совпадать.

В результате получим систему двух уравнений

Решая эту систему уравнений, имеем ; ,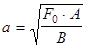

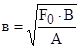
где F₀ — площадь отпечатка шины, которая определяется экспериментально;

А,В — стороны отпечатка, которые определяются экспериментально.

При отсутствии экспериментальных данных можно для грузовых автомобилей определить а и в по эмпирическим зависимостям:

* для тороидных шин 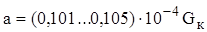, м

, м

· для широкопрофильных шин , м

, м

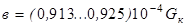
где G_к — нагрузка на колесо в Н.

Положение центра поворота отпечатка относительно его геометрического центра определяется плечом обкатки l₀ и плечом стабилизации у.

Под плечом обкатки понимается расстояние от центра поворота отпечатка, точки О, до большой оси отпечатка(см. рис.9.3). Согласно рис.9.3 плечо обкатки запишется

,

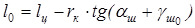
где l_ц — длина цапфы — расстояние между центрами шкворня и колеса;

a_ш -угол поперечного (бокового) наклона шкворня — угол между проекцией оси шкворня на поперечную плоскость автомобиля и вертикалью;

— угол развала колеса в нейтральном положении- угол между средней плоскостью колеса и вертикалью.

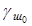
Под плечом стабилизации понимается расстояние от центра поворота, точки О, до малой оси отпечатка. Согласно рис.9.3 его определим по формуле

,

где 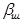— угол продольного наклона шкворня — угол между проекцией оси шкворня на продольную плоскость автомобиля и вертикалью.

Рис.9.3 Расчетная схема для определения положения центра поворота отпечатка

На рис.9.4 приведена экспериментальная зависимость М_j=(Q). Анализ экспериментальной зависимости момента сопротивления повороту шины на месте М_j от угла поворота Q показал, что эту зависимость можно условно разделить на три участка:

1-й АО — участок условной линейной зависимости момента М_j=(Q). На этом участке происходит упругое закручивание тела шины между отпечатком шины и жестким ободом. В контакте шины с опорной поверхностью на этом участке имеются только зоны сцепления, а зоны скольжения отсутствуют. На сухом асфальтобетоне первый участок находится в пределах 0 0 до 13 0 угла поворота колеса.

На втором участке момент М_j определяется по эмпирической зависимости

, (9.4)

где М_{j max} — предельный по сцеплению момент сопротивления повороту шины, который возникает при полном скольжении элементов шины, контактирующих с опорной поверхностью;

-наибольший угол поворота колеса на месте, при котором сохраняется условная линейная зависимость функции М_j =f(Q ;

— наименьший угол поворота колеса на месте, при котором момент сопротивления повороту шины достигает предельного значения М_{j max..}

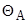
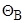
3-й ВС -участок предельного по сцеплению момента сопротивления повороту шины М_{j max}. На сухом асфальтобетоне третий участок начинается при повороте колеса на месте на угол более 13 о . На этом участке в контакте шины с опорной поверхностью имеются только зоны скольжения, а величина момента сопротивления повороту шины достигает максимального значения и не зависит от величины угла поворота. Практически во всех литературных источниках определяется момент сопротивления повороту шины на этом участке. Это объясняется в какой-то мере тем, что момент сопротивления повороту шины на этом участке достигает максимального значения. В дальнейшем по нему ведется расчет параметров рулевого управления автомобиля.

Для определения этого предельного момента примем следующие допущения:

— коэффициент сцепления и удельные давления в каждой точке отпечатка шины с опорной поверхностью одинаковы;

-отпечаток шины имеет форму прямоугольника.

На рис.9.5 приведена расчетная схема отпечатка шины для определения предельного по сцеплению момента сопротивления повороту шины. Точка О является центром поворота отпечатка (точка встречи оси шкворня с опорной поверхностью). Разобьем отпечаток шины на четыре прямоугольника с вершинами в точке О.

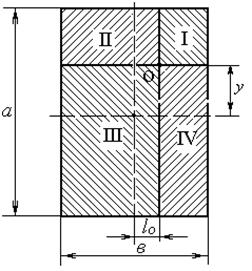Тогда прямоугольники, с учетом принятых обозначений, будут иметь стороны:

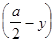
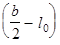
I прямоугольник — и ;

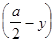
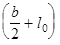
II прямоугольник — и ;

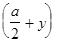
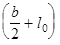
III прямоугольник — и ;

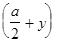
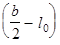
IV прямоугольник — и .

Рис.9.5 Расчетная схема отпечатка для определения момента

Согласно рис.9.5 момент сопротивления повороту всего отпечатка шины запишем

, (9.5.)

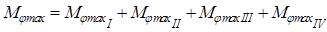
где 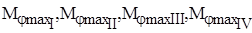-предельные по сцеплению моменты сопротивлению повороту отпечатков соответственно первого, второго, третьего, четвертого прямоугольников относительно центра поворота отпечатка, точки О.

Рассмотрим, в качестве примера, прямоугольник Ш. Для этого прямоугольника в общем случае момент сопротивления повороту определяется

по формуле ;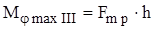

где F_тр — сила трения между отпечатком шины и опорной поверхностью.

Если учесть, что на недеформируемой поверхности коэффициент трения между шиной и опорной поверхностью является коэффициентом сцепления, тогда имеем 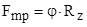₁₁₁ ,

где j — коэффициент сцепления;

R _{z 111} -нормальная реакция, действующая на ІІІ прямоугольник, которая равна

где S_III — площадь Ш прямоугольника ;

р — давление шины на опорную поверхность ;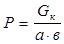

h — плечо действия силы F_тр.

Если учесть, что равнодействующая сил трения приложена в геометрическом центре прямоугольника III, тогда

.

После подстановки для третьего прямоугольника момент равен

. (9.6)

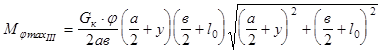
Окончательно с учетом (9.5) для всего отпечатка шины имеем

Если центр поворота отпечатка совпадает с его геометрическим центром, тогда l₀=y=0. После подстановки этих значений в уравнение (9.7) имеем

. (9.8)

Из анализа зависимостей (9.7) и (9.8) следует, что момент М_{j max} достигает минимального значения, если центр поворота отпечатка будет совпадать с его геометрическим центром. Смещение центра поворота отпечатка относительно его геометрического центра вызовет увеличение предельного по сцеплению момента сопротивления повороту шины. Для уменьшения этого смещения увеличивают угол поперечного наклона шкворня и уменьшают до нуля угол продольного наклона.

В ряде учебников по «Теории автомобиля» рекомендуют момент сопротивления повороту шины определять по зависимости (9.8), которая является частным случаем формулы (9.7). Зависимость (9.8) можно использовать только для частного случая, если центр поворота отпечатка (точка встречи оси шкворня с опорной поверхностью) совпадает с его геометрическим центром. Поскольку практически на всех автомобилях такие центры несовпадают, поэтому фактический момент различается от расчетного по зависимости (9.8) до 40%, что является недопустимым при проведении дальнейших расчетов параметров рулевых управлений.

Что же касается определения момента сопротивления повороту шины в полном диапазоне углов поворота колеса, то для его расчета необходимо использовать три зависимости:

— при углах поворота колеса от 0 0 до 5 0 зависимость (9.3);

— при углах поворота колеса от 5 0 до 13 0 зависимость (9.4);

— при углах поворота колеса от 13 0 и до максимального угла поворота зависимость (9.7)

Приведенные значения углов _А =5 0 и _В =13 0 максимальны и относятся к повороту шины на сухом асфальтобетоне. На опорных поверхностях, имеющих меньшее значение коэффициента сцепления, эти углы значительно меньшие.

1.Солтус А.П. Основы теории рабочего процесса и расчета колесных управляющих модулей (монография). Деп.Укр.НИИНТИ.№501-Ук90 ВИНИТИ «Деп.науч.труды»,1990, №7 (290),б/о 203.-234с., с.- 21-50

2. Гришкевич А.И. Автомобили: Теория.- Минск : Вышэйш шк.,1986.-240 с.,

3. Кошарний М.Ф. Основи механіки та енергетики автомобіля.-К.: Вища шк., 1992.-200 с., с. –128…155.

4. Литвинов А.С., Фаробин Я.Е. Автомобиль:Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-124…137.

1. Какие существуют способы изменения траектории движения автомобиля?

2. Какое назначение рулевой трапеции и рулевого управления?

3. Зачем уменьшают значение колеи передних колес в формуле, описывающей кинематику рулевой трапеции?

4. В каком случае при повороте колеса на месте не происходит его вращение относительно оси цапфы?

5. Из каких составляющих состоит момент сопротивления повороту колеса на месте?

6. Дайте анализ экспериментальной зависимости момента сопротивления повороту шины на месте от угла поворота.

7. Что такое предельный по сцеплению момент сопротивления повороту шины?

8. Перечислите факторы, влияющие на величину предельного по сцеплению момента сопротивления повороту шины.

9. В каком случае предельный по сцеплению момент сопротивления повороту шины минимальный?