Какое движение совершает колесо при движении автомобиля поступательное

2.1. Качение автомобильного колеса

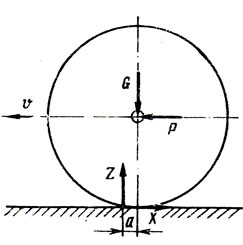
Основным преимуществом колеса как механизма является возможность экономии работы при перемещении груза за счет замены трения скольжения, возникающего на границе двух взаимно перемещаемых тел, значительно меньшим по величине трением качения. Действующие на колесо автомобиля силы и моменты вызывают со стороны дороги реактивные силы, которые в общем случае расположены в трех взаимно перпендикулярных направлениях и приложены к колесу в месте его контакта с основанием дороги. Эти реактивные силы получили название вертикальной G, тангенциальной X и боковой Y. Неподвижное колесо подвержено действию одной вертикальной силы G, приложенной к оси колеса (рис. 2.1). В этом случае действующая на ось колеса весовая нагрузка вызовет со стороны основания равную по величине реактивную силу Z. Вертикальная сила G, приложенная к оси колеса, и ее реакция Z со стороны дороги расположены в одной вертикальной плоскости, проходящей через ось колеса. Если приложить толкающую силу Р к автомобилю, он начнет перемещаться. Колесо начинает совершать вращательное движение относительно своего центра и поступательное перемещение относительно исходной точки дорожного основания. При этом сопротивления, возникающие при качении колеса, будут складываться из сопротивлений, препятствующих поступательному его перемещению.

Рис. 2.2. Силы, действующие на ведомое колесо

Качение колеса по опорной поверхности приводит к нарушению симметрии области контакта колеса и основания относительно вертикали, проходящей через центр колеса, и вызывает смещение реакции Z относительно этой вертикали вперед по ходу его движения на определенную величину а, называемую коэффициентом трения и измеряемую в единицах длины (рис. 2.2). Вертикальная реакция Z как и при неподвижном колесе, численно будет равна нагрузке.

Рис. 2.1. Действие сил на неподвижное жесткое колесо

В случае ведомого колеса толкающая сила Р от автомобиля через подшипник передается на ось колеса и вызывает со стороны основания тангенциальную реакцию X, которая будет приложена к поверхности колеса в зоне его контакта и будет иметь противоположное толкающей силе Р направление.

Описанный случай движения колеса характерен тем, что толкающая сила, действующая на его ось, обусловлена и всегда равна тем сопротивлениям, которые возникают при качении рассматриваемого колеса.

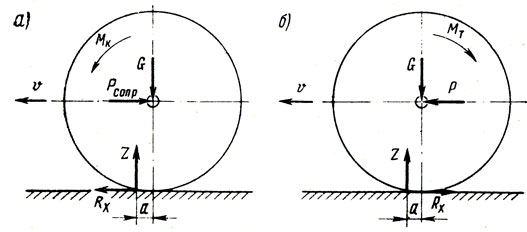
Работа ведущего колеса отличается тем, что к колесу прикладывается не толкающая сила, а крутящий момент (рис. 2.3, а). Этот момент М_к должен уравновесить суммарное сопротивление Р_сопр всех противодействующих движению сил (ветра, уклона дороги, трения, инерционных). В результате в контакте колеса с дорогой возникает реакция R_х = P_сопр, направленная в сторону движения.

Кроме функции ведомого и ведущего, колесо может выполнять роль тормозящего. Работу тормозящего колеса можно сравнить с работой ведущего. Разница состоит в том, что крутящий момент, а следовательно, и тангенциальная реакция дороги имеют противоположное направление и определяются интенсивностью торможения (рис. 2.3,б). Коэффициент сцепления между колесом и основанием в большинстве случаев значительно меньше единицы и, следовательно, тангенциальная сила, как правило, значительно меньше вертикальной.

Рис. 2.3. Силы, действующие на ведущее (а) и тормозящее (б) колесо

Толкающая сила, приложенная к оси ведомого колеса, и тангенциальная реакция, действующая на колесо со стороны основания, создают крутящий момент, который при установившемся движении равен моменту тангенциальной (или вертикальной) реакции относительно центра колеса. Для ведущего колеса крутящий момент складывается из суммы этих моментов, а для тормозящего колеса равен их разности.

Рис. 2.4. Действие сил на колеса во время движения по неровному основанию

Кроме перечисленных силовых факторов, колесо часто подвергается воздействию боковых сил и моментов, расположенных в плоскости, перпендикулярной плоскости вращения колеса.

На плоском и ровном основании боковые силы являются следствием действия на шасси автомобиля опрокидывающих поперечных сил, например центробежной силы на повороте или составляющей веса, обусловленной наклоном дороги.

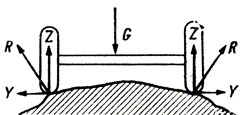
На выпуклом или вогнутом основании, а также при движении по дороге, имеющей неровности, колеса также могут испытывать действие боковых сил (рис. 2.4), которые при условии их равенства на левых и правых колесах по величине и противоположности по направлению будут гаситься на оси, не передаваясь на сам автомобиль. Действие на колесо боковой силы, так же как и тангенциальной, ограничено сцеплением колеса с дорогой. При движении автомобиля по выпуклому или вогнутому основанию или особенно по дороге с неровностями боковые силы могут достигать весьма значительной величины.

Таким образом, весь комплекс внешних нагрузок, действующих на колесо со стороны дороги, может быть представлен тремя взаимно перпендикулярными силовыми факторами:

вертикальной реакцией Z, величина которой обусловливается суммарным весом перевозимого груза и автомобиля. Эта нагрузка всегда действует на колесо независимо от того, движется оно или нет, работает в качестве ведомого, ведущего или тормозящего. Величина же этой нагрузки при движении может изменяться в зависимости от ускорения (замедления), продольного и поперечного профиля дороги, ее извилистости, неровностей дорожного полотна и скорости движения;

тангенциальной реакцией X, расположенной в плоскости колеса и являющейся следствием приложения к нему внешнего момента (крутящего или тормозного), толкающей силы, аэродинамического сопротивления, силы трения качения. Величина этой реакции достигает наибольшего значения обычно при торможении, однако, как правило, ограничена коэффициентом сцепления колеса с основанием дороги, который в большинстве случаев меньше единицы, а следовательно, даже наибольшее значение этой нагрузки, как правило, меньше вертикальной реакции;

боковой реакцией Y, которая расположена в плоскости, перпендикулярной плоскости колеса. Подобно тангенциальной эта нагрузка также ограничена силой сцепления колеса с дорогой и, следовательно, ее максимальное значение не может быть больше вертикальной силы, за исключением случаев движения по неровной дороге, глубокой колее. В этих условиях боковая сила может значительно превосходить силу сцепления колеса с дорогой.

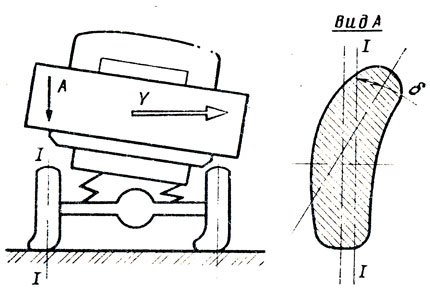
Рис. 2.5. Деформация шин при повороте автомобиля и соответствующее искажение пятна контакта шины с дорогой из-за увода колеса (вид А)

Особого интереса заслуживают качение наклоненного колеса и боковой увод шины. При движении автомобиля на повороте профиль эластичной шины деформируется в боковом направлении под действием центробежной силы, направленной перпендикулярно плоскости колеса (рис. 2.5). Вследствие боковой деформации шины колесо катится не в плоскости I-I, а под углом увода δ.

Способность шины к боковой деформации оказывает большое влияние на эксплуатационные свойства автомобиля, особенно на его устойчивость и управляемость. Поэтому параметры, определяющие увод колеса, являются важной характеристикой шины.

Увод колеса оценивается углом δ, который принято называть углом бокового увода. Приложенные к колесу силы вызывают боковую деформацию шины за счет изгиба протектора в боковом направлении. При качении колеса с уводом шина имеет сложную деформацию, которая несимметрична относительно ее вертикальной плоскости симметрии. При небольшой боковой силе и незначительных углах увода изменения боковой деформации в контакте подчиняются линейному закону.

Для каждой шины имеются определенная максимальная боковая сила и соответствующий ей определенный максимальный угол увода, при котором еще отсутствует большое проскальзывание элементов протектора в боковом направлении. Максимальный такой угол для большинства отечественных шин легковых автомобилей равен 3-5°.

Одним из часто встречающихся случаев качения колеса является случай движения его с наклоном к дороге. Действительно, на автомобиле колеса могут иметь наклон к дороге из-за их установки с разной нормальной деформацией шин, применения независимой подвески, наклона дороги и других факторов.

Наклон колеса к дороге оказывает существенное влияние на работу шины и траектории движения. При качении наклонного колеса в направлении плоскости вращения, со стороны дороги на него действуют так же, как и при уводе, боковая сила и момент. Последний стремится повернуть колесо в сторону его наклона.

Наклон колеса к дороге приводит к появлению боковой деформации шины, в результате которой центр давления контакта смещается в сторону наклона колеса. Возникают повышенные напряжения в плечевой зоне протектора шины. У наклонного колеса протектор шины изнашивается быстро и неравномерно, особенно в плечевой зоне со стороны наклона колеса. Таким образом, наклон колеса к дороге значительно уменьшает срок службы шины.

Наклон колеса к дороге изменяет угол увода. При движении автомобиля на повороте, когда при поперечном наклоне кузова колесо наклоняется в сторону боковой силы, увод колеса увеличивается. Такое явление наблюдается у передних управляемых колес легковых автомобилей, имеющих независимую подвеску. Уменьшение склонности шин к боковому уводу и уменьшение наклона колеса к дороге положительно сказываются на продлении срока службы шин. Уменьшения бокового увода можно достигнуть за счет увеличения ширины и понижения высоты профиля шины, увеличения угла наклона нитей корда по короне покрышки, повышения давления воздуха в шине, расширения обода.

Уменьшить наклон колес к дороге можно благодаря ряду конструктивных мер по установке колес, а также правильному подбору схемы и подвески. Целесообразно, чтобы подвеска при движении автомобиля на повороте создавала некоторый наклон колес к центру радиуса поворота автомобиля.

Влияние наклона колес в пределах практически встречающихся его величин на угол увода современных шин незначительно.

4 Кинематика и динамика автомобильного колеса

3.1. Общие сведения

3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.

3.3. Момент сопротивления качению эластичного колеса в ведомом режиме

3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению

3.1.Общие сведения

Энергия вращения, вырабатываемая двигателем автомобиля, преобразуется в поступательное движение транспортного средства движетелем, в качестве которого в автомобиле выступает система колес с эластичными пневматическими шинами.

Пневматическая шина представляет собой оболочку, напол­ненную сжатым воздухом. При каче­нии колеса по дороге происходит де­формация этой оболочки и проскальзывание элементов протектора относи­тельно поверхности дороги.

Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом r_c. Свободный радиус колеса — поло­вина наружного диаметра D_н;

Под наружным диаметром колеса понимается диаметр наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с доро­гой. Наружный диаметр колеса зави­сит от давления воздуха в шине и, как правило, возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или ка­талогах.

При действии на колесо вертикаль­ной нагрузки происходит деформация части шины, соприкасающейся с опор­ной поверхностью. При этом расстоя­ние от оси колеса до опорной поверх­ности становится меньше свободного радиуса. Это расстояние, замеренное у неподвижного колеса, называется ста­тическим радиусом r_ст. Статический радиус при номинальных нагрузках и давлении воздуха в шинах также ука­зывается в их характеристиках. Обыч­но шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13. 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:

где d — посадочный диаметр обода ши­ны;

l_z —коэффициент вертикальной деформации, зависящий от типа шин:

для тороидных шин l_z =0,85. 0,87;

для шин с регулируемым давлением и ароч­ных l_z =0,8. 0,85;

Н — высота профиля.

При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый колесом крутящий момент, скорость вра­щения и др.) расстояние между осью колеса и опорной поверхностью меня­ется. Это расстояние называют дина­мическим радиусом r_д. При качении ко­леса по твердой опорной поверхности с малой скоростью статический и ди­намический радиусы его практически одинаковы. Поэтому при приближен­ных расчетах динамический радиус ча­сто принимают равным статическому.

3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.

Реальное автомобильное колесо в тангенциальном направлении не является абсолютно жестким. Под воздействием передаваемого крутящего мо­мента протектор деформируется в тан­генциальном направлении. Если направление передаваемого момента совпадает с направлением угловой ско­рости колеса, элементы шины, находя­щиеся в набегающей полуокружности, подвергаются сжатию, а с противопо­ложной стороны — растяжению, как это показано на рис. 3.4. На этом же рисунке показана эпюра тангенциаль­ных напряжений в протекторе шины.

Рис. 3.4. Деформация шины (а) и эпюра на­пряжений в протекторе (б) при приложении к колесу крутящего момента:+ —зона сжатия; — —зона растяжения

Элементы шины, находящиеся в контакте с опорной поверхностью, нагружены в тангенциальном направле­нии неодинаково: элементы, входящие в контакт, сжимаются, а выходящие — растягиваются. При возрастании передаваемого крутящего момента увели­чивается площадь, в пределах которой происходит проскальзывание шины от­носительно дороги (рис. 3.5).

Рис. 3.5. Зависимость площади скольжения ко­леса (заштрихованная зона) от передаваемого им момента Мк

При не­котором значении момента начинается одновременное перемещение всех нахо­дящихся в зоне контакта точек колеса. Перемещение части точек колеса, на­ходящихся в контакте с дорожным по­крытием, относительно опорной по­верхности, когда в зоне контакта есть точки, неподвижные относительно этой поверхности, называется упругим про­скальзыванием колеса. Одновременное же перемещение всех находящихся в контакте точек колеса называется скольжением колеса.

Вследствие упругого проскальзывания или скольжения путь, проходи­мый колесом за один оборот, оказы­вается меньшим, чем путь, проходимый в ведомом режиме. При возрастании передаваемого крутящего момента уве­личивается тангенциальная деформа­ция шины и скольжение, а путь, проходимый колесом за один обо­рот, уменьшается.

Радиус качения колеса можно пред­ставить как радиус условного недеформируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реаль­ным колесом. Радиус качения колеса является условной величиной и непосредственно не связан с его размерами. Он определяется как отношение поступательной скорости колеса к угловой скорости его вращения r_k = v_x /w_k.

В соответствии с принятым выше определением, уменьшение пути центра колеса за определен­ное число его оборотов равносильно уменьшению радиуса качения.

Если направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возра­стать.

Рис. 3.6. Зависимость радиуса качения ко­леса от передаваемого ему крутящего момента

Зависимость радиуса качения ко­леса от передаваемого ему крутящего момента показана на рис. 3.6. На уча­стке 2—3 радиус качения линейно за­висит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу мо­менту:

где r_k0 — радиус качения при нулевом крутящем моменте, который соответ­ствует радиусу качения колеса в ведо­мом режиме;

l_t — коэффициент тан­генциальной эластичности шины, зави­сящий от типа и конструкции шины.

На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной ли­нией на графике показано, как изме­нялся бы радиус качения при отсутст­вии скольжения. Очевидно, что на участках 1—2 и 3—4 он может нахо­диться также по формуле (1.2). В по­следующем радиус качения, опреде­ленный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r₀.

На участках 0—1 и 4—5 происхо­дит полное скольжение элементов ши­ны относительно опорной поверхности. Точка 5 соответствует буксующему ко­лесу при неподвижном автомобиле, а точка 0—колесу, движущемуся юзом.

Если обозначить радиусы качения и переда­ваемые колесом моменты в начале и в конце линейного участка соответствен­но через М₂, r_к2 и М₃, r_к3, то коэффи­циент тангенциальной эластичности шины определим как

Экспериментально радиус качения находят путем определения числа обо­ротов колеса N на отрезке пути s при заданном режиме движения:

Согласно рис. 3.7, скорость точки В (скорость v_s) можно рассматривать как скорость скольжения элементов шины относительно опорной поверх­ности. В соответствии с принятыми обозначениями

Отсюда следует, что при r_к=r_о ко­лесо катится без скольжения. Если r_к>r_о, скорость скольжения положи­тельна и ее направление совпадает с направлением поступательной скорости колеса (колесо движется юзом). При r_к 2 ,

где f₀ — коэффициент сопротивления каче­нию при малой скорости. В тех случаях, когда действительное значение k_f неизвест­но, рекомендуется принимать k_f=7×10 -6

Температура шины. С увеличением тем­пературы шины ее сопротивление качению снижается, во-первых, за счет уменьшения гистерезисных потерь в резине, во-вторых, в результате повышения внутреннего дав­ления воздуха.

Рис. 3.12. Зависимость коэффициента сопротивления качению от температуры шины

При этом снижается коэф­фициент f в результате уменьшения дефор­маций шины (рис. 3.12). Приводимые в лите­ратуре значения f относятся обычно к пол­ностью прогретой шине.

Давление воздуха в шине р_в. Коэффициент f на различных дорогах в различной степени зависит от р_в. На доро­гах с твердым покрытием он уменьшается с увеличением давления р_в, достигая мини­мального значения при давлении р_в, близком к рекомендованному для данной шины. При чрезмерном давлении р_в воз­растают динамические нагрузки, возника­ющие в результате взаимодействия колеса с неровностями дороги, что может при­вести к некоторому возрастанию коэф­фициента f.

Рис. 3.13. Зависимость коэффициента сопротивления качению от внутреннего давления воздуха в шине на разных поверхностях: 1- песок; 2- пашня; 3- асфальт

Если движение происходит по деформи­руемым дорогам, при уменьшении давле­ния р_в увеличиваются потери, связанные с деформацией шины, но уменьшаются поте­ри, связанные с деформацией дороги. Можно подобрать такое давление р_в.опт, при котором сопротивление качению будет минимальным (рис. 3.13). Оптимальное дав­ление тем меньше, чем больше деформируемость дорожного полотна. Такая зави­симость коэффициента сопротивления ка­чению используется для повышения прохо­димости автомобилей с центральной системой регулирования давления в шинах.

Нагрузка на колесо Р_z. При неизменном давлении р_в увеличение Р_z приводит к возрастанию коэффициента f. На дорогах с твердым покрытием при изменении нагрузки в пределах 80. 110 % номинальной увеличение коэффициента f несущественно. При превышении нагруз­ки на 20 % номинального значения коэф­фициент возрастает приблизительно на 5 %, а при дальнейшей перегрузке — более интенсивно. Сильно возрастает ко­эффициент f с увеличением нагрузки Р_z на деформируемой опорной поверхности.

Конструктивные параметры шины. Зна­чение коэффициента f зависит от большо­го числа конструктивных параметров.

Увеличение толщины протектора повы­шает коэффициент f, особенно у диагональных шин. В связи с этим по мере из­носа шин сопротивление качению падает. При полностью изношенном протекторе сопротивление качению может уменьшить­ся на 20. 25 % по сравнению с неизно­шенным. У шин с вездеходным рисунком протектора, имеющих толщину протекто­ра почти в 2 раза большую, чем у шины с дорожным рисунком, при качении по доро­гам с твердым покрытием коэффициент f на 25. 30 % больше.

Уменьшение от­ношения высоты Н профиля шины к его ширине В приводит к снижению коэф­фициента сопротивления качению. Сниже­ние Н/В уменьшает также зависимость коэффициента f от скорости движения.

Внутреннее строение каркаса шины оказывает существенное влияние на коэффициент сопротивления качению. При v