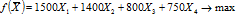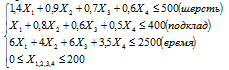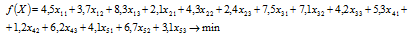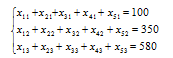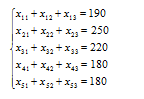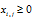Экономико-математические методы и модели
Автор работы: Пользователь скрыл имя, 12 Декабря 2012 в 22:26, задача
Описание работы
Задача №1
Пошивочное ателье собирается наладить выпуск повседневной одежды. При этом изделий каждого вида должно быть выпущено не более 200 штук.
В таблице приведены нормы расхода материалов на одно изделие, а также стоимость.
Составьте оптимальный план выпуска изделий пошивочной мастерской, при котором максимальна общая стоимость продукции. Спрос по каждому виду изделий не превышает 200 штук.
Задача №2
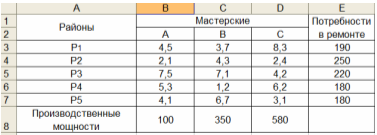
Имеются три специализированные мастерские по ремонту двигателей. Их производственные мощности равны соответственно 100, 350, 580 ремонтов в год. В пяти районах, обслуживаемых этими мастерскими, потребность в ремонте равна соответственно 190, 250, 220, 180, 180 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским следующие:
Спланируйте количество ремонтов каждой мастерской для каждого из районов, минимизирующее суммарные транспортные расходы.
Файлы: 1 файл
Решение.docx
Пошивочное ателье собирается наладить выпуск повседневной одежды. При этом изделий каждого вида должно быть выпущено не более 200 штук.
В таблице приведены нормы расхода материалов на одно изделие, а также стоимость.
Составьте оптимальный план выпуска изделий пошивочной мастерской, при котором максимальна общая стоимость продукции. Спрос по каждому виду изделий не превышает 200 штук.
Пусть переменные х1 – кол-во мужских брюк;
Целевая функция, определяющая общую стоимость продукции:
Для значений переменных назначаются ячейки В3:Е3. Коэффициенты целевой функции вводятся в ячейки В6:Е6. Ячейка целевой функции – Н7. В ней вводится функция СУММПРОИЗВ, Массив 1 В3:Е3, Массив 2 В6:Е6.
В ячейки В9:Е11 вводятся коэффициенты ограничений задачи, в ячейки G9:G11 вводятся правые части системы ограничений согласно условиям задачи. В ячейки H9:H11 вводятся правые части системы ограничений с помощью функции СУММПРОИЗВ, Массив 1 В3:Е3, Массив 2 В9:Е9 – В11:Е11.
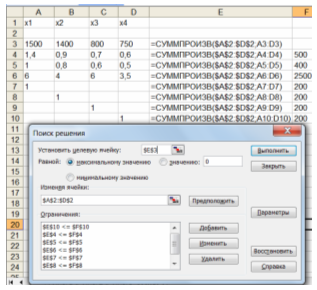
Далее открывается надстройка Поиск решения. В ней указывается целевая ячейка $Н$7, направление целевой функции «максимум», изменяемые ячейки переменных $В$2:$Е$2. Затем вводятся ограничения. Метод решения выбирается «Поиск решения линейных задач симплекс-методом».
Затем выполняется действие Найти решение. Появляется диалоговое окно, извещающее о том, что решение найдено.
Согласно найденному решению максимальная общая стоимость продукции составит 642300 руб. Для этого необходимо произвести 157 мужских брюк, 200 женских юбок, 200 детских юбок и отказаться от производства детских брюк.
Имеются три специализированные мастерские по ремонту двигателей. Их производственные мощности равны соответственно 100, 350, 580 ремонтов в год. В пяти районах, обслуживаемых этими мастерскими, потребность в ремонте равна соответственно 190, 250, 220, 180, 180 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским следующие:
Спланируйте количество ремонтов каждой мастерской для каждого из районов, минимизирующее суммарные транспортные расходы.
Пусть переменные х1j – кол-во ремонтов мастерской А для района Рj;
x2j – мастерской В для района Рj;
х3j – мастерской С для района Рj.
Целевая функция, определяющая суммарные транспортные расходы:
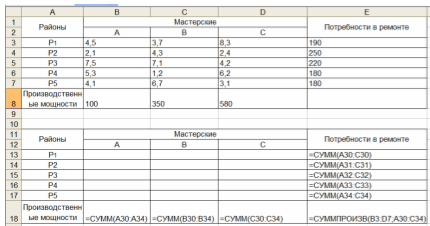
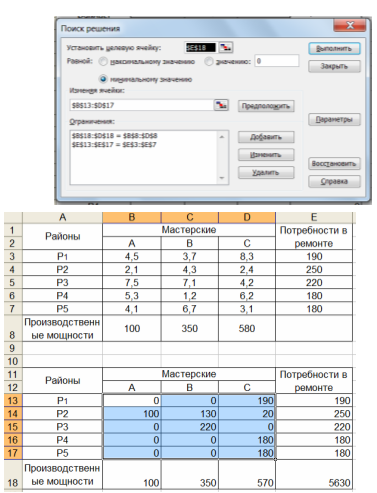
Формируется матрица ремонтов. Для этого в блок ячеек B3:D7 вводится «1». В ячейках B8:D8 будет отображаться общее количество ремонтов для каждой мастерской (через функцию СУММ). В ячейки B9:D9 вводятся производственные мощности мастерских. E3:E7 – количество ремонтов для каждого района (через функцию СУММ), F3:F7 – потребность в ремонте каждого района.
Затем в блок ячеек В13:D17 вводятся исходные данные.
Ячейкой целевой функции назначается G11. С помощью функции СУММПРОИЗВ выбираются массивы 1 — B3:D7; 2 — В13:D17.
Далее открывается надстройка Поиск решения. В ней указывается ячейка целевой функции $G$11, направление изменения целевой функции «минимум». Изменяемые ячейки переменных указываются $B$3:$D$7.
Затем вводятся ограничения. Метод решения выбирается Поиск решения линейных задач симплекс-методом.
Затем выполняется действие Найти решение. Появляется диалоговое окно, извещающее о том, что решение найдено.
Таким образом, получен план ремонтов, при котором суммарные транспортные расходы будут минимальны и составят 2022 ед. План означает, что:
- в мастерской А выполняются 100 заказов из района Р2;
- в мастерской В выполняются 350 заказов из района Р4;
- в мастерской С выполняются 580 заказов из района Р2.
Лабораторная работа: Лабораторная работа по Методам оптимальных решений Вариант №4
Тема: Лабораторная работа по Методам оптимальных решений Вариант №4
Тип: Лабораторная работа | Размер: 1.54M | Скачано: 147 | Добавлен 16.11.13 в 10:39 | Рейтинг: +1 | Еще Лабораторные работы
Вуз: Финансовый университет
Год и город: Уфа 2013
Задача 1
Пошивочное ателье собирается наладить выпуск повседневной одежды. При этом изделий каждого вида должно быть выпущено не более 200 штук. В таблице приведены нормы расхода материалов на одно изделие, а также стоимость.
Подкладочная ткань, м
Время на пошив, ч
Стоимость одного изделия, руб.
Составьте оптимальный план выпуска изделий пошивочной мастерской, при котором максимальна общая стоимость продукции. Спрос по каждому виду изделий не превышает 200 штук.
Решение.
Экономико-математическая модель задачи:
Х-число мужских брюк
Х-число женских юбок
Х-число детских брюк
Х-число детских юбок
Целевая функция:
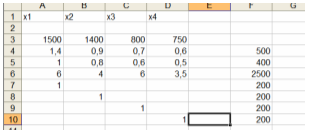
- Укажем адреса ячеек, в которые будет помещен результат решения. Оптимальные значения вектора Х поместим в ячейки A2:D2, а оптимальное значение целевой функции – в ячейке E3.
- Введем исходные данные.
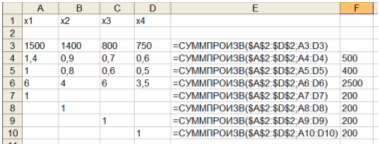
- Введем зависимость для целевой функции.
- Введем зависимости для ограничений.
- Запустим команду «Поиск решения».
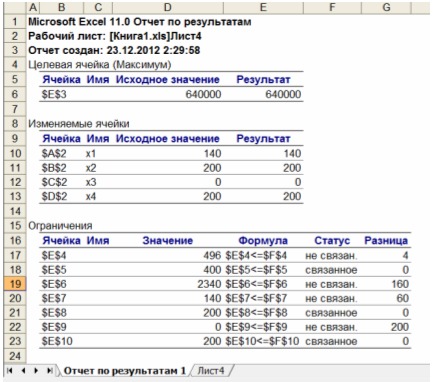
- В диалоговом окне «Результаты поиска решения» указываем тип отчета «Результаты».
Ответ. Необходимо сшить 140 мужских брюк, 200 женских юбок и 200 детских юбок, чтобы получить максимальную прибыль в 640 000 денежных единиц.
Задача 2
Имеются три специализированные мастерские по ремонту двигателей. Их производственные мощности равны соответственно 100, 350, 580 ремонтов в год. В пяти районах, обслуживаемых этими мастерскими, потребность в ремонте равна соответственно 190, 250, 220, 180, 180 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским следующие:
Спланируйте количество ремонтов каждой мастерской для каждого из районов, минимизирующее суммарные транспортные расходы.
Решение.
Так как целевая функция и неравенства-ограничения линейны, эта задача является задачей линейного программирования. Для ее решения применимы специальные методы, используемые для решения транспортных задач. Данная задача является транспортной задачей закрытого типа, так как необходимо использовать все производственные мощности и удовлетворить все потребности в ремонте.
Экономико-математическая модель задачи:
Переменные: – количество ремонтов j-той мастерской для i-того района.
Целевая функция – суммарные транспортные издержки, которые необходимо минимизировать:
- По производственным мощностям:
- По потребности в ремонте:
Прямые ограничения:
- Укажем адреса ячеек, в которые будет помещен результат решения. Изменяемые ячейки – В13: D17. В эти ячейки в результате решения задачи будут записаны оптимальные значения .
- Введем исходные данные задачи:
- Введем зависимости для ограничений.
- Введем зависимости для целевой функции.
- Запустим команду «Поиск решений».
Ответ. Распределение ремонтов мастерских для каждого из районов приведено выше. Общие затраты на транспортные расходы составят 5630 денежных единиц. Потребность в ремонте каждой мастерской удовлетворена полностью. Третья мастерская не реализовала 10 ремонтов.
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы
Примечание



Следует учитывать, что вследствие использования фиктивных тарифов реальнаяЦФ (то есть средства, которые в действительности придется заплатить за транспортировку муки) будет меньше формальнойЦФ на стоимость найденных в процессе решения фиктивных перевозок (на значение ячейки D5). Также необходимо учесть, что фиксированную поставку с первого склада на вторую пекарню в размере 4,5 т мы учли при составлении сбалансированной транспортной матрицы. В результате чего, полученное значение ЦФ необходимо увеличить на величину равную стоимости перевозки фиксированной перевозки.
Задачи для самостоятельного решения:
Задача 1. В хозяйстве на стойловый период заготовлено 1900 т сена, которое сосредоточено на трех участках .на 1 — 200 т, на 2 — 800 т, на 3 — 900 т. Сено перевозится на 4 фермы, потребности которых следующие: 1 — 300 т, 2 — 750 т, 3 — 550 т, 4-300 т. Себестоимость доставки 1 т сена от участка до фермы различна.
Себестоимость перевозки 1т сена, руб.
| Номер участка | Номер фермы >рмы |
Найти план перевозки сена от участков до ферм минимизирующий общую стоимость перевозок и удовлетворяющий полностью потребности ферм в сене.
Решить задачу методом северо-западного угла.
Задача 2. Имеются три специализированные мастерские по ремонту двигателей. Их производственные мощности равны соответственно 1100, 700 и 980 ремонтов в год. В пяти районах, обслуживаемых эти мастерские, потребность в ремонте равна соответственно 90, 180, 150, 120, 80 двигателей в год. Затраты на перевозку одного двигателя из районов к мастерским приведены в таблице.
Определить план прикрепления районов к ремонтным мастерским, обеспечивающий минимальные транспортные затраты.
| Районы | Мастерские | |
| 1 — ая | 2 — ая | 3 — ья |
| 4,5 2,1 7,5 5,3 4,1 | 2,7 4,3 3,1 1,9 6,7 | 8,3 2,4 4,2 6,2 3,1 |
Решить задачу методом минимального элемента по строке.
Задача № 3. Составить план распределения трех зерновых культур по участкам с различным почвенным плодородием. Обеспечивающий максимум валового сбора. Урожайность зерновых по типам и общая площадь посева отдельных культур приведены в таблице.
| Культуры | Урожайность по типам почв, ц/га | Общая площадь, га |
| Овес | ||
| Ячмень | ||
| Пшеница | ||
| Площадь участка, га |
Решить задачу методом северо-западного угла.
Задача № 4. Коммерческие банки Бi (i = 1, 4) выделяют предприятиям Пj (j = 1,4) кредиты на совершенствование производства с целью увеличения выпуска высококачественной продукции. Процентная ставка сij банка зависит от срока возмещения кредита. Естественно, что банки рассчитывают получить максимально возможную прибыль от использования кредитов предприятиями. Суммы Аi, которые банки могут выделить на кредиты, потребность предприятий Вj в кредитах и процентные ставки сij в расчете на 100 ден. ед. приведены в таблице. Найти оптимальное распределение банковских кредитов между предприятиями, максимизирующее общую прибыль, которую могут получить банки за пользование взятыми предприятиями кредитами.
Задача 5.На трёх станциях отправления А, В, С имеется соответственно 50, 20, 30 ед. однородного груза, который нужно доставить в 5 пунктов назначения согласно их потребностям. Эти данные, а также стоимость перевозки единицы груза от каждой станции отправления к каждому пункту назначения указаны в таблице.
| Пункты отправления | Запасы груза | Пункты назначения и их потребности | ||
| П1 | П2 | П3 | П4 | П5 |
| А | ||||
| В | ||||
| С |
Составить такой план перевозок грузов, чтобы затраты на эти перевозки были минимальными.

Задача 6.Менеджер транспортного отдела составляет план перевозок продукции фирмы в стандартных контейнерах на следующий месяц. Цены перевозок одного контейнера, величины заказов и запасы на складах даны в таблице.
Имеется 9 заказов от 9 потребителей. Заказы в сумме превышают запас на складах С1,…,С7. Найдите план перевозок, который минимизирует транспортные издержки. Как изменится план перевозок, если ввести запрет на перевозки с четвёртого склада третьему клиенту?
| Склады | Клиенты | Ресурсы | ||||||
| К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | К9 |
| С1 | ||||||||
| С2 | ||||||||
| С3 | ||||||||
| С4 | ||||||||
| С5 | ||||||||
| С6 | ||||||||
| С7 | ||||||||
| Заказ |
Задача 7.Менеджер-координатор аудиторской фирмы должен распределить аудиторов для работы на следующий месяц. Есть заявки от 10 клиентов на 75 аудиторов. В четырех конторах фирмы работают 90 аудиторов. 15 аудиторов можно отправить на плановую учебу. Аудиторы различаются по квалификации и опыту работы. Прежде чем приступить к аудиту конкретной фирмы, они должны затратить определенное время на подготовку и консультации.
Менеджер-координатор, учитывая опыт работы аудиторов каждой конторы, оценил время, необходимое в среднем аудитору каждой конторы для подготовки к аудиту конкретного клиента. Результаты приведены в таблице. Знаки вопроса в клетках таблицы означают, что аудиторы из этой конторы не имеют опыта аудита в отрасли, которой занимается данный клиент, и их нельзя к нему посылать. Распределить аудиторов так, чтобы суммарные временные затраты на подготовку были минимальны.
В реальной практике обычно требуют, чтобы аудиторы не все были из одной конторы. Попробуйте выполнить это условие и не слишком ухудшить решение.
| Конторы | Клиенты | Ресурсы | |||||||
| К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | К9 | К10 |
| А1. ГААПвилл | |||||||||
| А2. Финанстаун | |||||||||
| АЗ. ИСАбург | |||||||||
| А4. Нъю-Баланс | ? | ? | |||||||
| Заявки |
Задача 8.Менеджер транспортного отдела составляет план перевозок продукции фирмы в стандартных контейнерах на следующий месяц. Цены перевозок одного контейнера, величины заказов и запасы на складах даны в таблице.
| Склады | Ресурсы | Клиенты | |||||||
| К1 | К2 | К3 | К4 | К5 | К6 | К7 | К8 | К9 | К10 |
| С1 | |||||||||
| С2 | |||||||||
| С3 | |||||||||
| С4 | |||||||||
| Заказ |
Имеется 10 заказов от 10 потребителей. Заказы в сумме превышают запас на складах С1,…,С4. Найдите план перевозок, который минимизирует транспортные издержки.
Задача 9.Фирма имеет 4 фабрики и 5 центров распределения её товаров. Фабрики фирмы расположены в Барнауле, Ярославле ,Уфе и Чите с производственными возможностями 200, 150, 225, 175 единиц продукции ежедневно, соответственно. Центры распределения товаров фирмы располагаются в Москве, Курске, Омске, Томске, Иркутске с потребностями в 100, 200, 50, 250,150 единиц продукции ежедневно и соответственно. Хранение на фабрике единицы продукции не поставленной в центр распределения , обходиться в 0,75$ в день, а штраф за просроченную поставку единицы продукции, заказанной потребителем в центре распределения, но там не находящейся, равен 2,5$ в день. Стоимость перевозки единицы продукции с фабрик в пункты распределения приведена в таблице.
| Пункты | Москва | Курск | Омск | Томск | Иркутск |
| Барнаул | 1,5 | 1,75 | 2,25 | 2,25 | |
| Ярославль | 2,5 | 1,75 | 1,5 | ||
| Уфа | 1,5 | 1,5 | 1,75 | 1,75 | |
| Чита | 0,5 | 1,75 | 1,75 | 1,75 |
Необходимо спланировать перевозки так, чтобы суммарные транспортные расходы были минимальными.
Задача 10.Имеется три участка земли различной структуры и размера: 600, 180 и 220 га. С учетом демографического состава семей требуется построить не менее 290, 180, 110 и 420 домов различных проектов. Количество домов, которое можно разместить на одном гектаре площади, задается матрицей:
Сколько гектаров каждого участка следует застроить каждым видом домов, чтобы общее число домов было наибольшим?
По результатам выполнения лабораторной работы оформить отчет.
Структура отчета:
1. Титульный лист.
2. Основная часть.
Содержание основной части отчета: Кратко изложенное условие задачи; переменные задачи; уравнение целевой функции; критерий оптимальности; ограничения задачи с пояснениями. Экранные формы для решения (пустую и заполненную с результатами). Анализ полученных результатов.