Колёсная формула транспортного средства: полный привод и количество осей. Что такое колёсная формула?

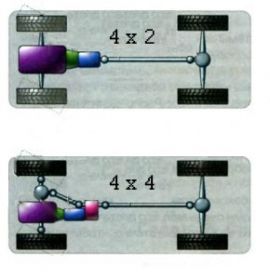
В продолжении темы про полный привод — использование универсального обозначения для быстрого обозначения особенности ходовой части. Это так называемая колёсная или осевая формула, или условное обозначение общего числа колёс транспортного средства и числа ведущих колёс двумя числами с использованием данных, где: [общее число колёс] × [число ведущих колёс], при этом спаренные колёса на одной полуоси учитываются как одно колесо. Например, колёсная формула 4×2 означает, что автомобиль имеет 4 колёса, 2 из которых ведущие. Автомобиль, обладающий полным приводом, имеет колёсную формулу, где оба числа одинаковы — 4×4, 6×6, 8×8, 10×10 и т. д.). Для многоосных автомобилей в колёсной формуле иногда указывают количество управляемых колёс, способных к повороту, например, 8×8/2). В этом случае третья цифра отделяется косой чертой, хотя иногда и применяется [×], с получением итоговой формулы 4х4х4, где четыре колеса ТС имеют полный привод и полноуправляемую систему поворота колёсами.

В том случае, если третья цифра 2 или 1 отделена от второй цифры точкой, то она указывает на тип ошиновки ведущей оси. Если используется цифра 2, значит ведущая задняя ось (оси, тележка) имеет двухскатную ошиновку, а цифра 1 указывает, что все колеса односкатные, таким образом, для двухосных грузовых автомобилей и автобусов применяются формулы 4х2.1. Использование в формуле колёс обозначения типа ошиновки, используется в основном на автомобилях производства Татра, например, 8х8.1, хотя не исключается и применение данной формулы у других производителей.

Есть и экзотические осевые формулы, помимо колёсного монстра на 12 осях производства МАЗ-7907 24×24/16, есть еще уникальные, но применяемые массово и серийно, это одноосные тягачи 2х2, предназначенные для буксировки полуприцепных несамоходных машин или оборудования, а также трехопорные тяговые машины 3х3. При использовании автопоезда, когда полуприцеп входит в состав транспортной единицы как его неотъемлемая часть, оси полуприцепа могут входит в формулу, а когда оси полуприцепа имеют активный привод, то данный автопоезд с активным полуприцепом обязательности вносит количество осей и приводных колёс полуприцепа в общую формулу.

Колёсная арифметика стандартизована, стандартом предусмотрены термины и понятия. Сегодня такая схема обозначения удобна, широко используется, и позволяет быстро понять, что за схема привода колёс используется на данном транспортном средстве. Помимо привода, важно понимать как устроена схема привода в совокупности с другим оборудованием и принципом реализации привода на колеса. Типичная трансмиссия современного автомобиля немыслима без дифференциала, позволяющего правому и левому ведущим колесам вращаться с разной скоростью, что совершенно необходимо для прохождения поворотов. Есть исключения, например в вездеходах и бронетехнике, как например несмотря на формуле колёс 8х8 схема привода использует всего один дифференциал. Но обычный симметричный дифференциал автомобиля и грузовика, разделяя крутящий момент поровну между полуосями, превращает колесную формулу в 4х1, стоит только одному из колес попасть на скользкую поверхность. Вот если бы создать на буксующем колесе сопротивление, притормозить его отдельно, тогда на второе колесо пойдет больший момент и оно, возможно, вытащит машину из беды. Но обычные тормоза действуют строго симметрично. Другое дело, если автомобиль оснащен электронной противобуксовочной системой с индивидуальными датчиками вращения колес и распределителем тормозного усилия. Умные тормоза способны «обмануть» простоватый дифференциал! Подобного эффекта можно добиться и механическими средствами, применив вместо обычного дифференциала так называемый кулачковый повышенного трения, который не допустит полной остановки одного из ведущих колес. Есть вариант попроще для конструкторов, но посложнее для водителей — обычный симметричный дифференциал. Его можно заблокировать принудительно. В соревновании механических и электронных устройств победа — за последними. Они надежнее, точнее и проще!

Массовые автомобили и грузовые транспортные средства чаще имеют задние ведущие колеса, поэтому первой получила распространение полноприводная схема с подключаемым передним мостом. Трансмиссия усложнялась вначале лишь ради повышения внедорожных качеств, поэтому о межосевом дифференциале еще не думали (в грязи и на снегу небольшая пробуксовка просто незаметна). В итоге родилась схема популярного до сих пор Уаза, которая массово применяется в армейской технике. И не надо думать, что она осталась лишь на «полуармейских» вездеходах. Так устроены, например, и вполне гражданские внедорожники и кроссоверы. Если автомобиль изначально проектировался как переднеприводный, то не исключен и вариант с подключаемым задним мостом: таков, например внедорожник ЛуАЗ.

С такой схемой привода вседорожника полный привод в раздаточной коробке можно подключить прямо на ходу, остальное сделают автоматические муфты на колесах. Конструкторы многих внедорожников обошлись вообще без обгонных муфт, отключая передние колеса «у основания» их приводов. В УАЗах еще остались муфты с ручным включением, требующие обязательной экипировки водителя болотными сапогами. Вообще говоря, эти муфты если и нужны, то лишь для автомобилей, проводящих большую часть жизни на шоссе: благодаря им приводы отключенных от двигателя (но не от дороги!) колес не вращаются зазря и, стало быть, не изнашиваются. Ну, и расход топлива чуть уменьшается. Кстати, авторы ЛуАЗа, предназначенного в первую очередь для сельской глубинки, создавая свой вездеход, никаких муфт не ставили, не забыв, однако, о колесных редукторах, увеличивающих дорожный просвет этого компактного, но высокопроходимого вездехода. Из-за отсутствия межосевого дифференциала включать такой полный привод стоит только на бездорожье, причем ненадолго, и двигаться не быстрее 60 км/ч. Компенсацией за неудобства владельцу служат лучшие внедорожные качества «проходимца».

Но помимо привода на четыре колеса, есть внедорожные транспортные средства и вездеходы, включая грузовые автомобили с колесной формулой 6х6 и 8х8, которые обладают завидной проходимостью, но — какой ценой и сложностью! Чтобы полностью реализовать возможности трансмиссии и нормально двигаться по дороге, трехосной машине нужны пять дифференциалов, и четырехосной уже шесть дифференциалов, желательно самоблокирующихся или хотя бы с принудительной блокировкой, а еще хорошо бы вовсе отключать пару мостов, когда они не нужны.

Для облегчения управления полным приводом в многоосных машинах используеться автоматическое управление трансмиссией (ADM — Automatic Drive-train Management), разработанное в технологическом центре фирмы «Штайр», что сделало прорыв на рынке тяжелых внедорожников. Автоматика не только включает при необходимости передний мост, но и блокирует межосевой и все межколесные дифференциалы. Причем делает это не по жесткой программе, последовательно вводя все больше блокировок, а по командам компьютера, получающего информацию о пробуксовке каждого колеса. При этом учитываются траектория движения автомобиля (едет ли он по прямой или поворачивает), необходимость резкого ускорения, если водитель нажал на газ до упора, коэффициент сцепления с дорогой каждой шины. Как только дорожные условия улучшаются, блокировки и полный привод «сами собой» отключаются. На испытаниях вся система работала настолько хорошо, как будто за рулем сидел ас триала! А ведь на самом деле у водителя не было ни одного дополнительного рычага или кнопочки. В сочетании с автоматической коробкой передач шоферу остаются только две педали да баранка. А с ними справится даже новичок, что особенно важно для армии и служб спасения.

Итак, автоматика и электроника постепенно вытесняют из автомобиля не только педали и рычаг коробки передач, но и дополнительные органы управления сложной полноприводной трансмиссией.

Колесная формула автомобилей, автобусов, грузовиков

Колесная формула автомобиля содержит два показателя – общее число колес и количество ведущих. Значительно реже формулу могут дополнять наклонная черта или точка. Рассмотрим каждый вариант подробно с примерами.

Распространенная формула

Если говорить о колесной формуле легковых автомобилей, обычно это 4х2 или 4х4. Первое число обозначает общее количество колес, а второе говорит о количестве ведущих. Следовательно, 4х2 (четыре на два) – автомобиль имеет 4 колеса, 2 из них ведущие. У полноприводных оба числа будут одинаковыми (4х4, 8х8, 16х16).

В интернете можно встретить записи вида 2х4 (два на четыре), с формулировкой, что для переднего привода сначала указывают ведущие колеса. Чтобы проверить эту теорию, перед публикацией статьи мы посетили официальные сайты отечественных и зарубежных автопроизводителей. Подтверждений не нашлось, у всех в технических характеристиках первым идет количество колес.

Отсюда простой вывод: колесной формулы переднего привода нет, она одна для всех.

Формула с косой чертой

У грузовых автомобилей, после второго показателя (количества ведущих колес) может присутствовать еще один, отделенный от основной формулы косой чертой. Например, грузовик повышенной проходимости Урал-5323, имеет колесную формулу 8х8/4. Это значит все 8 колес ведущие, а цифра 4 говорит о том, что половина из них управляемые.

Важно помнить, что даже если на полуоси находится 2 колеса, в формуле они указываются как одно. Поэтому по первому показателю легко узнать количество осей транспортного средства:

• 8 – четырехосные;
• 6 – трехосные;
• 4 – двухосные.

Формула с точкой

Часто в формуле для грузовиков и автобусов встречается точка, после которой стоят цифры 1 или 2. По записи подобного вида можно определить ошиновку ведущего моста. Цифра 2 говорит о двухскатной ошиновке (2 колеса на полуось). Если стоит 1 – все мосты односкатные.

Название пошло от старого обозначения колес – скаты.

Специально для автобусов Икарус (в простонародье «гармошки»), в колесную формулу добавили четвертую цифру, также отделенную точкой. Она характеризует ошиновку прицепной части автобуса. Возможные вариации: 1 и 2.

Другая техника

Трактора

Формула для тракторов имеет свои особенности. Нередко встречаются варианты 4к2, 4к2а, 4к4б. Как и в случае с автомобилями, первая цифра указывает на количество колес, вторая на ведущие. Литера А после цифры сообщает о меньшем диаметре передней колесной пары, Б о равных диаметрах передних и задних колес.

Автогрейдеры

Автогрейдер – прицепная или самоходная машина, предназначенная для перемещения и разравнивания сыпучих материалов, снега. В колесной формуле для автогрейдеров указывается количество осей. Возьмем запись типа АхБхВ, где:

• А – число управляемых осей;
• Б – количество ведущих осей;
• В – общее количество.

Таким образом формула 1х2х2 читается как: полноприводный, двухосный грейдер с одной поворотной осью.

Таблицы

В таблицах вы найдете формулы самых распространенных транспортных средств. Два и более показателя через запятую, говорят о наличии у производителя различных модификаций.

4 Кинематика и динамика автомобильного колеса

3.1. Общие сведения

3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.

3.3. Момент сопротивления качению эластичного колеса в ведомом режиме

3.4. Влияние конструктивных и эксплутационных факторов на коэффициент сопротивления качению

3.1.Общие сведения

Энергия вращения, вырабатываемая двигателем автомобиля, преобразуется в поступательное движение транспортного средства движетелем, в качестве которого в автомобиле выступает система колес с эластичными пневматическими шинами.

Пневматическая шина представляет собой оболочку, напол­ненную сжатым воздухом. При каче­нии колеса по дороге происходит де­формация этой оболочки и проскальзывание элементов протектора относи­тельно поверхности дороги.

Размер автомобильного колеса в свободном, ненагруженном состоянии характеризуется свободным радиусом r_c. Свободный радиус колеса — поло­вина наружного диаметра D_н;

Под наружным диаметром колеса понимается диаметр наибольшего окружного сечения беговой дорожки колеса при отсутствии контакта с доро­гой. Наружный диаметр колеса зави­сит от давления воздуха в шине и, как правило, возрастает с его увеличением, определяется непосредственно замером. Значение наружного диаметра колеса при номинальном давлении воздуха в шине указывается в ГОСТах или ка­талогах.

При действии на колесо вертикаль­ной нагрузки происходит деформация части шины, соприкасающейся с опор­ной поверхностью. При этом расстоя­ние от оси колеса до опорной поверх­ности становится меньше свободного радиуса. Это расстояние, замеренное у неподвижного колеса, называется ста­тическим радиусом r_ст. Статический радиус при номинальных нагрузках и давлении воздуха в шинах также ука­зывается в их характеристиках. Обыч­но шины конструируют таким образом, чтобы при номинальных нагрузке и давлении прогиб шины составлял 13. 20 % от высоты профиля. Статический радиус при известных конструктивных параметрах шин можно находить из соотношения:

где d — посадочный диаметр обода ши­ны;

l_z —коэффициент вертикальной деформации, зависящий от типа шин:

для тороидных шин l_z =0,85. 0,87;

для шин с регулируемым давлением и ароч­ных l_z =0,8. 0,85;

Н — высота профиля.

При качении нагруженного колеса в силу ряда причин (динамическое действие нагрузки, передаваемый колесом крутящий момент, скорость вра­щения и др.) расстояние между осью колеса и опорной поверхностью меня­ется. Это расстояние называют дина­мическим радиусом r_д. При качении ко­леса по твердой опорной поверхности с малой скоростью статический и ди­намический радиусы его практически одинаковы. Поэтому при приближен­ных расчетах динамический радиус ча­сто принимают равным статическому.

3.2. Упугое проскальзывание и скольжение колеса. Радиус качения колеса.

Реальное автомобильное колесо в тангенциальном направлении не является абсолютно жестким. Под воздействием передаваемого крутящего мо­мента протектор деформируется в тан­генциальном направлении. Если направление передаваемого момента совпадает с направлением угловой ско­рости колеса, элементы шины, находя­щиеся в набегающей полуокружности, подвергаются сжатию, а с противопо­ложной стороны — растяжению, как это показано на рис. 3.4. На этом же рисунке показана эпюра тангенциаль­ных напряжений в протекторе шины.

Рис. 3.4. Деформация шины (а) и эпюра на­пряжений в протекторе (б) при приложении к колесу крутящего момента:+ —зона сжатия; — —зона растяжения

Элементы шины, находящиеся в контакте с опорной поверхностью, нагружены в тангенциальном направле­нии неодинаково: элементы, входящие в контакт, сжимаются, а выходящие — растягиваются. При возрастании передаваемого крутящего момента увели­чивается площадь, в пределах которой происходит проскальзывание шины от­носительно дороги (рис. 3.5).

Рис. 3.5. Зависимость площади скольжения ко­леса (заштрихованная зона) от передаваемого им момента Мк

При не­котором значении момента начинается одновременное перемещение всех нахо­дящихся в зоне контакта точек колеса. Перемещение части точек колеса, на­ходящихся в контакте с дорожным по­крытием, относительно опорной по­верхности, когда в зоне контакта есть точки, неподвижные относительно этой поверхности, называется упругим про­скальзыванием колеса. Одновременное же перемещение всех находящихся в контакте точек колеса называется скольжением колеса.

Вследствие упругого проскальзывания или скольжения путь, проходи­мый колесом за один оборот, оказы­вается меньшим, чем путь, проходимый в ведомом режиме. При возрастании передаваемого крутящего момента уве­личивается тангенциальная деформа­ция шины и скольжение, а путь, проходимый колесом за один обо­рот, уменьшается.

Радиус качения колеса можно пред­ставить как радиус условного недеформируемого кольца, которое, катясь без скольжения, совершит число оборотов и пройдет путь, одинаковый с реаль­ным колесом. Радиус качения колеса является условной величиной и непосредственно не связан с его размерами. Он определяется как отношение поступательной скорости колеса к угловой скорости его вращения r_k = v_x /w_k.

В соответствии с принятым выше определением, уменьшение пути центра колеса за определен­ное число его оборотов равносильно уменьшению радиуса качения.

Если направление передаваемого момента будет противоположным направлению угловой скорости вращения колеса (тормозящее колесо), при увеличении момента радиус качения будет возра­стать.

Рис. 3.6. Зависимость радиуса качения ко­леса от передаваемого ему крутящего момента

Зависимость радиуса качения ко­леса от передаваемого ему крутящего момента показана на рис. 3.6. На уча­стке 2—3 радиус качения линейно за­висит от передаваемого момента, и его изменение определяется упругим проскальзыванием колеса. Акад. Е. А. Чудаковым, впервые установившим эту зависимость, предложена следующая формула для нахождения радиуса качения по передаваемому колесу мо­менту:

где r_k0 — радиус качения при нулевом крутящем моменте, который соответ­ствует радиусу качения колеса в ведо­мом режиме;

l_t — коэффициент тан­генциальной эластичности шины, зави­сящий от типа и конструкции шины.

На участках 1—2 и 3—4 изменение радиуса качения определяется как упругим проскальзыванием, так и скольжением колеса. Пунктирной ли­нией на графике показано, как изме­нялся бы радиус качения при отсутст­вии скольжения. Очевидно, что на участках 1—2 и 3—4 он может нахо­диться также по формуле (1.2). В по­следующем радиус качения, опреде­ленный при отсутствии скольжения, будем называть радиусом качения без скольжения и обозначать r₀.

На участках 0—1 и 4—5 происхо­дит полное скольжение элементов ши­ны относительно опорной поверхности. Точка 5 соответствует буксующему ко­лесу при неподвижном автомобиле, а точка 0—колесу, движущемуся юзом.

Если обозначить радиусы качения и переда­ваемые колесом моменты в начале и в конце линейного участка соответствен­но через М₂, r_к2 и М₃, r_к3, то коэффи­циент тангенциальной эластичности шины определим как

Экспериментально радиус качения находят путем определения числа обо­ротов колеса N на отрезке пути s при заданном режиме движения:

Согласно рис. 3.7, скорость точки В (скорость v_s) можно рассматривать как скорость скольжения элементов шины относительно опорной поверх­ности. В соответствии с принятыми обозначениями

Отсюда следует, что при r_к=r_о ко­лесо катится без скольжения. Если r_к>r_о, скорость скольжения положи­тельна и ее направление совпадает с направлением поступательной скорости колеса (колесо движется юзом). При r_к 2 ,

где f₀ — коэффициент сопротивления каче­нию при малой скорости. В тех случаях, когда действительное значение k_f неизвест­но, рекомендуется принимать k_f=7×10 -6

Температура шины. С увеличением тем­пературы шины ее сопротивление качению снижается, во-первых, за счет уменьшения гистерезисных потерь в резине, во-вторых, в результате повышения внутреннего дав­ления воздуха.

Рис. 3.12. Зависимость коэффициента сопротивления качению от температуры шины

При этом снижается коэф­фициент f в результате уменьшения дефор­маций шины (рис. 3.12). Приводимые в лите­ратуре значения f относятся обычно к пол­ностью прогретой шине.

Давление воздуха в шине р_в. Коэффициент f на различных дорогах в различной степени зависит от р_в. На доро­гах с твердым покрытием он уменьшается с увеличением давления р_в, достигая мини­мального значения при давлении р_в, близком к рекомендованному для данной шины. При чрезмерном давлении р_в воз­растают динамические нагрузки, возника­ющие в результате взаимодействия колеса с неровностями дороги, что может при­вести к некоторому возрастанию коэф­фициента f.

Рис. 3.13. Зависимость коэффициента сопротивления качению от внутреннего давления воздуха в шине на разных поверхностях: 1- песок; 2- пашня; 3- асфальт

Если движение происходит по деформи­руемым дорогам, при уменьшении давле­ния р_в увеличиваются потери, связанные с деформацией шины, но уменьшаются поте­ри, связанные с деформацией дороги. Можно подобрать такое давление р_в.опт, при котором сопротивление качению будет минимальным (рис. 3.13). Оптимальное дав­ление тем меньше, чем больше деформируемость дорожного полотна. Такая зави­симость коэффициента сопротивления ка­чению используется для повышения прохо­димости автомобилей с центральной системой регулирования давления в шинах.

Нагрузка на колесо Р_z. При неизменном давлении р_в увеличение Р_z приводит к возрастанию коэффициента f. На дорогах с твердым покрытием при изменении нагрузки в пределах 80. 110 % номинальной увеличение коэффициента f несущественно. При превышении нагруз­ки на 20 % номинального значения коэф­фициент возрастает приблизительно на 5 %, а при дальнейшей перегрузке — более интенсивно. Сильно возрастает ко­эффициент f с увеличением нагрузки Р_z на деформируемой опорной поверхности.

Конструктивные параметры шины. Зна­чение коэффициента f зависит от большо­го числа конструктивных параметров.

Увеличение толщины протектора повы­шает коэффициент f, особенно у диагональных шин. В связи с этим по мере из­носа шин сопротивление качению падает. При полностью изношенном протекторе сопротивление качению может уменьшить­ся на 20. 25 % по сравнению с неизно­шенным. У шин с вездеходным рисунком протектора, имеющих толщину протекто­ра почти в 2 раза большую, чем у шины с дорожным рисунком, при качении по доро­гам с твердым покрытием коэффициент f на 25. 30 % больше.

Уменьшение от­ношения высоты Н профиля шины к его ширине В приводит к снижению коэф­фициента сопротивления качению. Сниже­ние Н/В уменьшает также зависимость коэффициента f от скорости движения.

Внутреннее строение каркаса шины оказывает существенное влияние на коэффициент сопротивления качению. При v