Cхема замещения асинхронного электродвигателя

Трехфазные асинхронные электродвигатели, или как их еще называют индукционные электродвигатели, являются наиболее распространенными в промышленности. Данный тип электродвигателя, аналогично машинам постоянного тока тоже обладают свойствами обратимости, и может работать как в двигательном, генераторном, так и в тормозных режимах – противовключение, динамическое торможение. Режим работы асинхронного электродвигателя характеризуют знаком и величиной скольжения.

Пожалуй, основным методом анализа установившихся режимов индукционного электродвигателя является использование эквивалентных схем замещения. В таком случае обычно рассматривают явление, которое относится к одной фазе многофазного двигателя при соединении его обмоток звездой.

Упрощенная картина магнитных потоков работающего асинхронного электродвигателя позволяет представить его в виде эквивалентной схемы:

Электромагнитная связь первичной и вторичной цепи осуществляется потоком взаимоиндукции Ф, индуктирующим в роторной обмотке ЭДС Е₂S. Сопротивление индуктивное первичной цепи Х₁ обусловлено наличием потока рассеивания, связанного только с этой цепью. Аналогично сопротивления Х₂ обусловлено потоком рассеивания Ф₂₅.

Частота тока ротора будет определяться скоростью его вращения относительно скорости вращения магнитного поля статора, то есть зависеть от скольжения и будет равна f₂ = f₁S.

Ток вторичной цепи при вращающемся роторе:

Также выражения для I₂ может иметь:

Выше показанные выражения имеют не только различную форму записи, но и имеют совершенно разный физический смысл. А смысл его в том, что вместо вращающегося ротора можно рассматривать неподвижный, в котором будет индуцироваться ЭДС Е₂. При этом индуктивное сопротивление будет равно Х₂, а активное возрастет на величину так как . При этом I₁ останется прежним по фазе и величине, что не повлияет на потребляемую из сети мощность. Поскольку I₁ и I₂ не изменятся, то естественно и потери в первичных и вторичных цепях также не изменятся, соответственно мощность тоже не будет изменяться, а мощность развиваемая двигателем при вращении, будет равна мощности, потребляемой в добавочном сопротивлении . Таким образом, эквивалентная схема замещения асинхронной машины может быть заменена схемой замещения с добавочным сопротивлением r_д во вторичной цепи:

Т – образная схема замещения

После приведения первичной и вторичной ЭДС они будут равны Е₁ = Е₂ / и это дает возможность соединить эквивалентные точки и получить такую схему:

Недостатком Т – образной схемы замещения помимо сложностей расчета, является зависимость всех токов I₁, I₂ / , I_μ от скольжения s.

Из Т – образной схемы замещения видно, что в режиме холостого хода, при I₂ / = 0 и s = 0, ток в контуре будет обуславливаться сопротивлениями намагничивающего контура и первичной цепи и совсем не будет зависеть от скольжения. Данное обстоятельство позволит вынести на зажимы электродвигателя намагничивающий контур и перейти к Г – образной схеме замещения.

Г – образная схема замещения

Данная схема замещения позволяет изучать процессы в асинхронном электродвигателе, которые имеют место при изменении скольжения электрической машины.

Учет контура намагничивания необходим при определении I₁, который потребляется из сети. Но Г — образная схема замещения будет справедлива лишь при наличии определенных допущений:

• Все цепи имеют неизменные (постоянные) параметры. Это значит, что приведенное вторичное сопротивление r₂ / не будет зависеть от частоты цепи вторичной (ротора), а насыщение не будет влиять на реактивное сопротивление статорных и роторных обмоток Х₁ и Х₂ / ;
• Полная проводимость намагничивающего контура принимается неизменной, а ток намагничивания, независимо от нагрузки, будет всегда пропорционален напряжению, приложенному к обмоткам;
• Потери добавочные не учитываются;
• Паразитные моменты, создаваемые высшими гармониками МДС, также не учитывают.

Следует также помнить и то, что в Г – образной схеме замещения в величины сопротивлений необходимо внести соответствующие поправки:

В выше перечисленных уравнениях величины имеющие индекс «дейст» соответствуют реальным значениям параметров асинхронной машины, а без индексов – те, которые используют в эквивалентной схеме.

Поскольку отношение r₁/x_μ довольно таки мало, то практически довольно часто принимают:

Обычно δ лежит в пределах 1,05 – 1,1.

Первичный ток I₁ будет равен при любом скольжении:

Приведенный роторный ток:

Показанное выше выражение показывает, что ток ротора является функцией скольжения. При s = 0 I₂ / = 0. При увеличении скольжения I₂ / также будет расти, а при s = 1 достигнет своего максимума, или тока короткого замыкания, или пускового:

Если в роторной цепи отсутствует добавочное сопротивление (АД с КЗ ротором), пусковой ток может достигнуть довольно приличных значений, а именно 5 – 8 раз больше чем его номинальное значение.

Данная зависимость показана ниже:

Отношения пускового значения к номинальному является очень важным параметром для асинхронных машин с короткозамкнутым ротором, так как наличие пусковых токов приводит к просадкам напряжения, что особо ощутимо при использовании электродвигателей средней и большой мощности. Поэтому данная характеристика приводится в каталогах по выбору электрических машин.

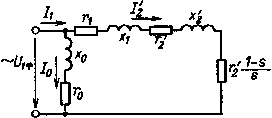
Схема замещения асинхронного двигателя

При практических расчетах вместо реального асинхронного двигателя, на схеме его заменяют эквивалентной схемой замещения, в которой электромагнитная связь заменена на электрическую. При этом параметры цепи ротора приводятся к параметрам цепи статора.

По сути, схема замещения асинхронного двигателя аналогична схеме замещения трансформатора. Различие в том, что у асинхронного двигателя электрическая энергия преобразуется в механическую энергию (а не в электрическую, как это происходит в трансформаторе), поэтому на схеме замещения добавляют переменное активное сопротивление r₂ ‘ (1-s)/s, которое зависит от скольжения. В трансформаторе, аналогом этого сопротивления является сопротивление нагрузки Z н .

Величина скольжения определяет переменное сопротивление, например, при отсутствии нагрузки на валу, скольжение практически равно нулю s≈0, а значит переменное сопротивление равно бесконечности, что соответствует режиму холостого хода. И наоборот, при перегрузке двигателя, s=1, а значит сопротивление равно нулю, что соответствует режиму короткого замыкания.

Как и у трансформатора, у асинхронного двигателя есть Т-образная схема замещения.

Более удобной при практических расчетах является Г-образная схема замещения.

В Г-образной схеме, намагничивающая ветвь вынесена к входным зажимам. Таким образом, вместо трех ветвей получают две ветви, первая – намагничивающая, а вторая – рабочая. Но данное действие требует внесение дополнительного коэффициента c₁, который представляет собой отношение напряжения подводимого к двигателю, к ЭДС статора.

Величина c₁ приблизительно равна 1, поэтому для максимального упрощения, на практике принимают значение c₁≈1. При этом следует учитывать, что значение коэффициента c₁ уменьшается с увеличением мощности двигателя, поэтому более точное приближение будет соответствовать более мощному двигателю.

Параметры схемы замещения рассматриваются подробнее в статье векторная диаграмма асинхронного двигателя

СХЕМА ЗАМЕЩЕНИЯ АСИНХРОННОГО ДВИГАТЕЛЯ

Для анализа работы асинхронного двигателя пользуются схемой замещения. Схема замещения асинхронного двигателя аналогична схеме замещения трансформатора и представляет собой электрическую схему, в которой вторичная цепь (обмотка ротора) соединена с первичной цепью (обмоткой статора) гальванически вместо магнитной связи, существующей в двигателе.

Рис. 10.17. Схема замещения асинхронного двигателя

Основное отличие асинхронного двигателя от трансформатора в энергетическом отношении состоит в следующем. Если в трансформаторе энергия, переданная переменным магнитным полем во вторичную цепь, поступает к потребителю в виде электрической энергии, то в асинхронном двигателе энергия, переданная вращающимся магнитным полем ротору, преобразуется в механическую и отдается валом двигателя потребителю в виде механической энергии.

Электромагнитные мощности, передаваемые магнитным полем во вторичную цепь трансформатора и ротору двигателя, имеют одинаковые выражения:

В трансформаторе электромагнитная мощность за вычетом потерь во вторичной обмотке поступает к потребителю:

где r_п — сопротивление потребителя. В асинхронном двигателе электромагнитная мощность за вычетом потерь в обмотке ротора превращается в механическую мощность:

Подставив в (10.47) вместо Р ее значение из (10.42), получим

Pмех=3I2 2	r2(1 — s)	=3I’2 2	r’2(1 — s)	= 3I2 2 r’э = 3I’2 2 r’э,
s	s
где r’э = r’2	1 — s	.
s

Сравнивая выражения (10.46) и (10.48), можно заключить, что

Таким образом, потери мощности в сопротивлении r’_э численно равны механической мощности, развиваемой двигателем.

Заменив в схеме замещения трансформатора сопротивление нагрузки r’_п на r’_э = r’₂ (1 — s)/s,получим схему замещения асинхронного двигателя (рис. 10.17). Все остальные элементы схемы замещения аналогичны соответствующим элементам схемы замещения трансформатора: r₁, х₁ — активное сопротивление и индуктивное сопротивление рассеяния фазы обмотки статора; r’₂, х’₂— приведенные к обмотке статора активное сопротивление и индуктивное сопротивление рассеяния фазы обмотки ротора.

Приведенные значения определяются так же, как и для трансформатора:

Может возникнуть сомнение в возможности использования гальванической связи цепей статора и ротора в схеме замещения, поскольку частоты в этих цепях на первый взгляд не одинаковы. Первая часть схемы замещения представляет собой эквивалентную схему фазы обмотки ротора, которая, как было показано в § 10.7, приведена к частоте тока статора. В реальном же двигателе в отличие от схемы замещения частоты тока ротора и статора не одинаковы.